Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-23T13:46:20.826Z Has data issue: false hasContentIssue false
  • English
  • Français

On the existence of sulutions of the equation Lx ∞ Nx and a coincidence degree theory

Published online by Cambridge University Press:  09 April 2009

E. Tarafdar  and
Suat Khoh Teo
E. Tarafdar
Affiliation:
Department of Mathematics University of Queensland St Lucia, Queensland 4067, Australia
Suat Khoh Teo
Affiliation:
Department of Mathematics University of Queensland St Lucia, Queensland 4067, Australia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The coincidence degree for the pair (L, N) developed by Mawhin (1972) provides a method for proving the existence of solutions of the equation Lx = Nx where L: dom L ⊂ X → Z is a linear Fredholm mapping of index zero and is a (possiblv nonlinear) mapping and Ω is a bounded open subset of X, X and Z being normed linear spaces over the reals. In this paper we have extended the coincidence degree for the pair (L, N) to solve the equation 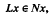, where L: dom L ⊂ X → Z is a linear Fredholm mapping of index zero, 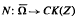and X, Z and Ω are as above, CK(Z) being the set of compact convex subsets of Z.

Subject classification (Amer. Math. Soc. (MOS) 1970): primary 47 H 15, 47 A 50; secondary 47 H 10, 47 A 55.

Keywords

Set-valued compact vector fieldset-valued ultimately compact vector fieldk-ϕ-contractionscoincidence degree.
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 28 , Issue 2 , September 1979 , pp. 139 - 173
Copyright
Copyright © Australian Mathematical Society 1979

References

Bartle, R. G. (1953), ‘Singular points of functional equations’, Trans. Amcr. Math. Soc. 75, 366–384.CrossRefGoogle Scholar
Borisovich, G. Yu. and Saironov, I. Yu. (1968) ‘A contribution to the topological theory of condensing operators’, Soviet Math. Dokl 9, 1304–1308.Google Scholar
Bancroft, S., Hale, J. K. and Sweet, D. (1968), ‘Alternative problems for nonlinear functional equations’, J. Differential Equations 4, 40–56.CrossRefGoogle Scholar
Cacciopoli, R. (1946), ‘Sulle corespondenze funzionali inverse diramate: teoria generate e applicazioni ad alcune equazioni funzionali non lineari e al problema di plateau’, Atti Acad. Naz. Lincei, Rend. Cl. Sci. Fis. Mat. Natur. 24, 258–268, 416–421.Google Scholar
Cellina, A. and Lasota, A. (1969), ‘A new approach to the definition of topological degree for multivalued mappings’, Atti Acad. Naz. Lincei Rend. Cl. Sci. Fis. Mat. Natur. (8) 47, 434–440.Google Scholar
Cesari, L. (1963), ‘Functional analysis and periodic solutions of nonlinear differential equations’, Contributions to Differential Equations 1, 149–187.Google Scholar
Cesari, L. (1964), Functional analysis and Galerkin's method, Michigan Math. J. II 385–418.Google Scholar
Cesari, L. (1969), ‘Functional analysis and differential equations’, Siam Studies in Applied Mathematics 5, 143–155.Google Scholar
Cesari, L. (1971), ‘Functional analysis and boundary value problems’, in: Analytic thory in differential equations pp. 178–194 (Springer-Verlag Lecture Notes No. 183).Google Scholar
Cronin, J. (1950), Branch points of solutions of equations in Banach spaces’, Trans. Amer. Math. Soc. 69, 208–231.CrossRefGoogle Scholar
Danes, J. (1974), ‘On densifying and related mappings and their application in nonlinear functional analysis’, in Theory of nonlinear operators, pp. 15–56 (Proceedings of a Summer School, Akademic-Verlag, Berlin).Google Scholar
Dolph, C. L. and Minty, G. J. (1964), ‘On nonlinear integral equations of the Hammerstein type’ in: Integral equations, pp. 99–154 (Madison University Press, Madison, Wisconsin).Google Scholar
Dugundji, J., ‘An extension of Tietze's theorem’, Pacific J. Math. 1, 353–376.CrossRefGoogle Scholar
Ehrmann, H. (1965), ‘Existanzsatze für die Lösungen gewisser nichtlinearer Randwertaufgaben’, S. Angew. Math. Mech. 45, 22–39: Abh. Deutsch Akad. Wiss. Berlin Kl. Math. Phys. Tech., 157–167.Google Scholar
Gaines, R. E. and Mawhin, J. L. (1977), Coincidence degree and nonlinear differential equations (No. 568, Springer-Verlag Lecture Notes).CrossRefGoogle Scholar
Granas, A. (1959), ‘Sur la notion du degre topologique pour une certaine classe de transformations multivalentes dans les espaces de Banach’, Bull. Acad. Polon. Sci. Sir. Sci. Math. Astronom. Phys. 7, 191–194.Google Scholar
Hale, J. K. (1969), Ordinary differential equations (Wiley-Interscience, New York).Google Scholar
Hale, J. K. (1971), Applications of alternative problems (Lecture Notes 71–1. Brown University, Providence, R.I.).CrossRefGoogle Scholar
Hetzer, G. (1975), ‘Some remarks on ϕ + operators and on the coincidence degree for a Fredholm equation with noncompact nonlinear perturbation’, Ann. Soc. Sci. Bruxelles Sér. 1, 89, 497–508.Google Scholar
Hetzer, G. (1975), ‘Some applications of the coincidence degree for set-contractions to functional differential equations of neutral type’, Comm. Math. Univ. Carolinae, 16, 121–138.Google Scholar
Locker, J. (1967), ‘An existence analysis for nonlinear equations in Hilbert space’, Trans. Amer. Math. Soc. 128, 403–413.CrossRefGoogle Scholar
Ma, T. W. (1972), ‘Topological degree for set-valued compact vector fields in locally convex spaces’, Dissertationes Math. 92, 1–43.Google Scholar
Mawhin, J. L. (1972), ‘Equivalence theorem for nonlinear operator equations and coincidence degree for some mappings in locally convex topological vector spaces’, J. Differential Equations, 12, 610–636.CrossRefGoogle Scholar
Nagumo, M. (1951), ‘Degree of mapping in convex linear topological spaces’, Amer. J. Math. 73, 497–511.CrossRefGoogle Scholar
Nirenberg, L. (1960–1961), Functional analysis (New York Univ. Lecture Notes).Google Scholar
Nussbaum, R. D. (1969), The fixed point index and fixed point theorems for k-set-contractions (Doctoral Dissertation, University of Chicago. Chicago, 111.).CrossRefGoogle Scholar
Nussbaum, R. D. (1971), ‘The fixed point index for condensing maps’, Ann. Mat. Pura Appl. 89, 217–258.CrossRefGoogle Scholar
Petryshyn, W. V. and Fitzpatrick, P. M. (1974), ‘A degree theory, fixed point theorems, and mapping theorems for multivalued noncompact mappings’, Trans. Amer. Math. Soc. 194, 1–25.CrossRefGoogle Scholar
Sadovskii, B. N. (1968), ‘Measures of noncompactness and condensing operators’, Problemy Mat. Anal. Sloz. Sistem, 2, 89–119.Google Scholar
Sadovskii, B. N. (1972), ‘Ultimately compact and condensing operators’, Russian Math. Surveys, 27, 85–156.CrossRefGoogle Scholar
Shimizu, T. (1948), ‘Analytic operations and analytic operational equations’ Math. Japan, 1, 36–40.Google Scholar
Vainberg, M. M. and Aizengendler, P. G. (1968), ‘The theory and methods of investigation of branch points of solutions’, in: Progress in mathematics, vol. II, 1–72 (Penum, New York).Google Scholar
Vainberg, M. M. and Trenogin, V. A. (1962), ‘The methods of Lyapunov and Schmidt in the theory of nonlinear equations and their further development’, Russian Math. Surveys, 17, 1–60.CrossRefGoogle Scholar
Vainikko, G. M. and Sadovskii, B. N. (1968), ‘On the degree of (Ball) condensing vector fields’, Problemy Mat. Anal. Slov. Sistem, 2, 84–88.Google Scholar
Williams, S. A. (1968), ‘A connection between the Cesari and Leray-Schauder methods’, Michigan Math. J. 15, 441–448.CrossRefGoogle Scholar