Hostname: page-component-f554764f5-fr72s Total loading time: 0 Render date: 2025-04-13T06:45:03.472Z Has data issue: false hasContentIssue false
  • English
  • Français

On the distribution of the time to first emptiness of a store with stochastic input

Published online by Cambridge University Press:  09 April 2009

A. M. Hasofer
A. M. Hasofer
Affiliation:
University of Tasmania, Australia.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Kendall [4] has given for the distribution of the time to first emptiness in a store with an input process which is homogeneous and has non-negative independent increments and an output of one unit per unit time the formula . In this formula, z is the initial content of the store, g(t, z) is the density function of the time to first emptiness τ(z), defined by 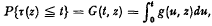and k(t, x) is the density function of the input process ξ(t), defined by .

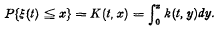Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 4 , Issue 4 , November 1964 , pp. 506 - 517
Copyright
Copyright © Australian Mathematical Society 1964

References

[1]Beněs, V. E. (1957), On queues with Poisson arrivals, Ann. Math. Stat. 28, 670–677.CrossRefGoogle Scholar
[2]Gnedenko, B. V. and Kolmogorov, A. N. (1954), Limit Distributions for Sums of Independent Random Variables, Addison-Wesley, Cambridge, Mass.Google Scholar
[3]Kingman, J. F. C. (1963), On continuous time models in the theory of dams, this Journal 3, 480–87.Google Scholar
[4]Kendall, D. G. (1957), Some problems in the theory of dams, J. R. Statist. Soc. B, 19, 207–212.Google Scholar
[5]Lloyd, E. H. (1963), The epochs of emptiness of a semi-infinite discrete reservoir, J. R. Statist. Soc. B, 25, 131–136.Google Scholar
[6]Loève, M. (1960), Probability Theory, (2nd ed.) Van Nostrand, Princeton.Google Scholar
[7]Widder, D. V. (1941), The Laplace Transform, Princeton University Press.Google Scholar