No CrossRef data available.
Published online by Cambridge University Press: 09 April 2009
It is known that the theory of Cauchy's problem for differential equations with two independent variables is réducible to the corresponding problem for systems of quasi-linear equations. The reduction is carried further, by means of the theory of characteristics, to the case of systems of equations of the special form first considered by H. Lewy [1]. The simplest case is that of the pair of equations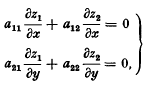 where the aii depend on z1 and z2. The problem to be considered is that of finding functions z1(x, y), z2(x, y) which satisfy (1) and which take prescribed values on x + y = 0.
where the aii depend on z1 and z2. The problem to be considered is that of finding functions z1(x, y), z2(x, y) which satisfy (1) and which take prescribed values on x + y = 0.