Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Soni, K.
and
Soni, R. P.
1973.
Lipschitz Behavior and Characteristic Functions.
SIAM Journal on Mathematical Analysis,
Vol. 4,
Issue. 2,
p.
302.
Soni, Kusum
and
Soni, R.P.
1974.
A tauberian theorem related to the modified Hankel transform.
Bulletin of the Australian Mathematical Society,
Vol. 11,
Issue. 2,
p.
167.
Ridenhour, J. R.
and
Soni, R. P.
1974.
Parseval Relation and Tauberian Theorems for the Hankel Transform.
SIAM Journal on Mathematical Analysis,
Vol. 5,
Issue. 5,
p.
809.
Bingham, N. H.
and
Doney, R. A.
1974.
Asymptotic properties of supercritical branching processes I: The Galton-Watson process.
Advances in Applied Probability,
Vol. 6,
Issue. 4,
p.
711.
Soni, K
and
Soni, R.P
1975.
Slowly varying functions and asymptotic behavior of a class of integral transforms III.
Journal of Mathematical Analysis and Applications,
Vol. 49,
Issue. 3,
p.
612.
Soni, K
and
Soni, R.P
1975.
Slowly varying functions and asymptotic behavior of a class of integral transforms. II.
Journal of Mathematical Analysis and Applications,
Vol. 49,
Issue. 2,
p.
477.
Soni, K
and
Soni, R.P
1975.
Slowly varying functions and asymptotic behavior of a class of integral transforms I.
Journal of Mathematical Analysis and Applications,
Vol. 49,
Issue. 1,
p.
166.
Emery, D. J.
1975.
On a condition satisfied by certain random walks.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 31,
Issue. 2,
p.
125.
Haan, Laurens De
1977.
On functions derived from regularly varying functions.
Journal of the Australian Mathematical Society,
Vol. 23,
Issue. 4,
p.
431.
Luther, Wolfram
1977.
�ber das asymptotische Verhalten der trigonometrischen und Hankelschen Integraltransformation.
Archiv der Mathematik,
Vol. 29,
Issue. 1,
p.
614.
Hall, Peter
1978.
On the rate of convergence of moments in the central limit theorem.
Journal of the Australian Mathematical Society,
Vol. 25,
Issue. 2,
p.
250.
Miroshin, R. N.
1978.
Conditions of Local Nondeterminism of Differentiable Gaussian Stationary Processes.
Theory of Probability & Its Applications,
Vol. 22,
Issue. 4,
p.
831.
Hall, Peter
1979.
On the rate of convergence in the central limit theorem for distributions with regularly varying tails.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 49,
Issue. 1,
p.
1.
Malevich, T. L.
1980.
On Conditions for the Moments of the Number of Zeros of Gaussian Stationary Processes to Be Finite.
Theory of Probability & Its Applications,
Vol. 24,
Issue. 4,
p.
741.
Doney, R.A.
1982.
On the exact asymptotic behaviour of the distribution of ladder epochs.
Stochastic Processes and their Applications,
Vol. 12,
Issue. 2,
p.
203.
Frenk, J. B. G.
1982.
The behavior of the renewal sequence in case the tail of the waiting-time distribution is regularly varying with index −1.
Advances in Applied Probability,
Vol. 14,
Issue. 4,
p.
870.
Pitman, E. J. G.
1982.
The Making of Statisticians.
p.
111.
Frenk, J. B. G.
1982.
The behavior of the renewal sequence in case the tail of the waiting-time distribution is regularly varying with index −1.
Advances in Applied Probability,
Vol. 14,
Issue. 4,
p.
870.
Malevich, T. L.
1985.
On Conditions for Finiteness of the Factorial Moments of the Number of Zeros of Gaussian Stationary Processes.
Theory of Probability & Its Applications,
Vol. 29,
Issue. 3,
p.
534.
Welsh, A. H.
1986.
ON THE USE OF THE EMPIRICAL DISTRIBUTION AND CHARACTERISTIC FUNCTION TO ESTIMATE PARAMETERS OF REGULAR VARIATION.
Australian Journal of Statistics,
Vol. 28,
Issue. 2,
p.
173.
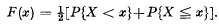 . In mathematical analysis it is a little more convenient to use this function rather than
. In mathematical analysis it is a little more convenient to use this function rather than 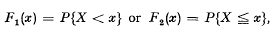 , which arise more naturally in probability theory. In all cases we shall consider
, which arise more naturally in probability theory. In all cases we shall consider 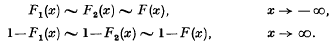 With this definition, if the distribution function of X is F(x), then the distribution function of −X is 1−F(−x). The distribution of X is symmetrical about 0 if F(x) = 1 − F(−x).
With this definition, if the distribution function of X is F(x), then the distribution function of −X is 1−F(−x). The distribution of X is symmetrical about 0 if F(x) = 1 − F(−x).