Hostname: page-component-f554764f5-nwwvg Total loading time: 0 Render date: 2025-04-11T17:39:31.118Z Has data issue: false hasContentIssue false
  • English
  • Français

On the average number of real zeros of a class of random algebraic equations

Part of: Combinatorics

Published online by Cambridge University Press:  09 April 2009

N. N. Nayak  and
S. Bagh
N. N. Nayak
Affiliation:
Orissa University of Agricultureand Technology Bhubaneswar, 751003 Orissa, India
S. Bagh
Affiliation:
Department of StatisticsSambalput UniversityJyoti Vihar, 768019 Orissa, India
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let g1, g2, …, gn be a sequence of mutually independent, normally distributed, random variables with mathematical expectation zero and variance unity. In this work, we obtain the average number of real zeros of the random algebraic equations Σnk=1 Kσ gk(ω)tk = C, where C is a constant independent of t and not necessarily zero. This average is (1/π) 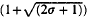log n, when n is large and σ is non-negative.

MSC classification

Secondary: 05A17: Partitions of integers 05A19: Combinatorial identities, bijective combinatorics
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 49 , Issue 1 , August 1990 , pp. 149 - 160
Copyright
Copyright © Australian Mathematical Society 1990

References

Logan, B. F. and Shepp, L. A. (1968), ‘Real zeros of random polynomials II’, Proc. London Math. Soc. (3) 18, 306–314.Google Scholar
Williamson, B. (1955), The integral calculus, (Scientific Book Company, Patna, India).Google Scholar
Cramer, H. (1954), Mathematical methods of statistics, (Princeton University Press).Google Scholar
Farahmand, K. (1986), ‘On the average number of real roots of a random algebraic equation’, Ann. Probab. 14, 702–709.CrossRefGoogle Scholar
Das, M. (1969), ‘The average number of maxima of a random algebraic curve’, Proc. Cambridge Philos. Soc. 65, 741–753.CrossRefGoogle Scholar
Kac, M. (1943), ‘On the average number of real roots of a random algebraic equation’, Bull. Amer. Math. Soc. 49, 314–320.CrossRefGoogle Scholar
Kac, M. (1959), Probability and related topics in physical sciences, (Interscience, New York).Google Scholar