Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Мафи, Амир
Mafi, Amir
Сареми, Еро
and
Saremi, Hero
2013.
Конечность градуированных модулей обобщенных локальных когомологий.
Математические заметки,
Vol. 94,
Issue. 5,
p.
689.
Mafi, A.
and
Saremi, H.
2013.
Finiteness of graded generalized local cohomology modules.
Mathematical Notes,
Vol. 94,
Issue. 5-6,
p.
642.


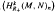 be the
be the 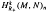 . In this paper we study the asymptotic behavior of Assf
. In this paper we study the asymptotic behavior of Assf 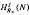 is not finitely generated.
is not finitely generated.