Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-02-05T20:30:25.409Z Has data issue: false hasContentIssue false
  • English
  • Français

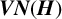ON THE ALGEBRAS $\boldsymbol {VN(H)}$ AND 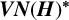$\boldsymbol {VN(H)^{*}} $ OF AN ULTRASPHERICAL HYPERGROUP 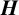$\boldsymbol {H}$

Part of: Commutative Banach algebras and commutative topological algebras Abstract harmonic analysis

Published online by Cambridge University Press:  12 December 2022

REZA ESMAILVANDI ,
MEHDI NEMATI  and
NAGESWARAN SHRAVAN KUMAR Open the ORCID record for NAGESWARAN SHRAVAN KUMAR [Opens in a new window]
REZA ESMAILVANDI
Affiliation:
Department of Mathematical Sciences, Isfahan Uinversity of Technology, Isfahan 84156-83111, Iran and Instituto Universitario de Matemáticas y Aplicaciones (IMAC), Universidad Jaume I, Castellón, E-12071, Spain e-mail: [email protected], [email protected]
MEHDI NEMATI
Affiliation:
Department of Mathematical Sciences, Isfahan Uinversity of Technology, Isfahan 84156-83111, Iran and School of Mathematics, Institute for Research in Fundamental Sciences (IPM), PO Box 19395-5746, Tehran, Iran e-mail: [email protected]
NAGESWARAN SHRAVAN KUMAR*
Affiliation:
Department of Mathematics, Indian Institute of Technology Delhi, New Delhi 110016, India
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let H be an ultraspherical hypergroup and let 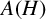$A(H)$ be the Fourier algebra associated with 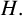$H.$ In this paper, we study the dual and the double dual of 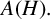$A(H).$ We prove among other things that the subspace of all uniformly continuous functionals on 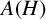$A(H)$ forms a 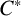$C^*$-algebra. We also prove that the double dual 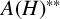$A(H)^{\ast \ast }$ is neither commutative nor semisimple with respect to the Arens product, unless the underlying hypergroup H is finite. Finally, we study the unit elements of 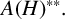$A(H)^{\ast \ast }.$

Keywords

Fourier algebrasultraspherical hypergroupslocally compact groupsuniformly continuous functionals

MSC classification

Primary: 43A62: Hypergroups 43A30: Fourier and Fourier-Stieltjes transforms on nonabelian groups and on semigroups, etc. 43A60: Almost periodic functions on groups and semigroups and their generalizations (recurrent functions, distal functions, etc.); almost automorphic functions
Secondary: 43A07: Means on groups, semigroups, etc.; amenable groups 46J10: Banach algebras of continuous functions, function algebras
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 115 , Issue 3 , December 2023 , pp. 337 - 353
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by George Willis

References

Akeman, C. A. and Walter, M. E., ‘Non-abelian Pontriagin duality’, Duke Math. J. 39 (1972), 451–463.Google Scholar
Alaghmandan, M., ‘Remarks on weak amenability of hypergroups’, Preprint, 2018, arXiv:1808.03805.Google Scholar
Bonsall, F. F. and Duncan, J., Complete Normed Algebras (Springer, New York, 1973).CrossRefGoogle Scholar
Dales, H. G., Banach Algebras and Automatic Continuity, London Mathematical Society Monographs, 24 (Clarendon Press, Oxford, 2000).Google Scholar
Dales, H. G. and Lau, A. T.-M., ‘The second dual of Beurling algebras’, Mem. Amer. Math. Soc. 177(836) (2005), vi+191.Google Scholar
Damek, E. and Ricci, F., ‘Harmonic analysis on solvable extensions of H-type groups’, J. Geom. Anal. 2 (1992), 213–248.CrossRefGoogle Scholar
Degenfeld-Schonburg, S., Kaniuth, E. and Lasser, R., ‘Spectral synthesis in Fourier algebras of ultraspherical hypergroups’, J. Fourier Anal. Appl. 20 (2014), 258–281.CrossRefGoogle Scholar
Dixmier, J., C*-Algebras (North-Holland Publishing Co., Amsterdam–New York–Oxford, 1977).Google Scholar
Dunkl, C. F. and Ramirez, D. E., ‘Weakly almost periodic functionals on the Fourier algebra’, Trans. Amer. Math. Soc. 185 (1973), 501–514.CrossRefGoogle Scholar
Esmailvandi, R. and Nemati, M., ‘Multipliers and uniformly continuous functionals over Fourier algebras of ultraspherical hypergroups’, Filomat. 35(9) (2021), 3139–3150.CrossRefGoogle Scholar
Esmailvandi, R. and Nemati, M., ‘Compact and weakly compact multipliers over Fourier algebras of ultraspherical hypergroups’, Mediterr. J. Math. 18 (2021), 33; doi:10.1007/s00009-020-01651-y.CrossRefGoogle Scholar
Eymard, P., ‘L’algèbre de Fourier d’un groupe localement compact’, Bull. Soc. Math. France 92 (1964), 181–236.CrossRefGoogle Scholar
Granirer, E. E., ‘Weakly almost periodic and uniformly continuous functionals on the Fourier algebra of any locally compact group’, Trans. Amer. Math. Soc. 189 (1974), 371–382.CrossRefGoogle Scholar
Granirer, E. E., ‘Density theorems for some linear subspaces and some C*-algebras of $VN(G)$ ’, Symp. Math. Istit. Naz. Alta Mat. XXII (1977), 61–70.Google Scholar
Jewett, R. I., ‘Spaces with an abstract convolution of measures’, Adv. Math. 18 (1975), 1–101.CrossRefGoogle Scholar
Kaniuth, K. and Lau, A. T.-M., Fourier and Fourier–Stieljes Algebras on Locally Compact Groups, Mathematical Surveys and Monographs, 231 (American Mathematical Society, Providence, RI, 2018).CrossRefGoogle Scholar
Lau, A. T.-M., ‘The second conjugate algebra of the Fourier algebra of a locally compact group’, Trans. Amer. Math. Soc. 267 (1981), 53–63.CrossRefGoogle Scholar
Lau, A. T.-M., Loy, R. J. and Willis, G. A., ‘Amenability of Banach and C*-algebras on locally compact groups’, Studia Math. 119 (1996), 161–178.Google Scholar
Megginson, R. E., An Introduction to Banach Space Theory (Springer-Verlag, New York, 1998).CrossRefGoogle Scholar
Miao, T., ‘Unit elements in the double dual of a subalgebra of the Fourier algebra $A(G)$ ’, Canad. J. Math. 61 (2009), 382–394.CrossRefGoogle Scholar
Michael, E., ‘Topologies on spaces of subsets’, Trans. Amer. Math. Soc. 71 (1951), 152–182.CrossRefGoogle Scholar
Muruganandam, V., ‘Fourier algebra of a hypergroup. $\mathrm{II}.$ Spherical hypergroups’, Math. Nachr. 11 (2008), 1590–1603.CrossRefGoogle Scholar
Shravan Kumar, N., ‘Invariant means on a class of von Neumann algebras related to ultraspherical hypergroups’, Studia Math. 225 (2014), 235–247.CrossRefGoogle Scholar
Shravan Kumar, N., ‘Invariant means on a class of von Neumann algebras related to ultraspherical hypergroups II’, Canad. Math. Bull. 60 (2017), 402–410.CrossRefGoogle Scholar