In the development of the rotor calculus presented in a previous paper space-time was taken to be flat. This work is now extended to the case of curved space-times, which, in the first instance, is taken to be Riemannian. (The calculus bears at times a strong formal resemblance to the spinor analysis of Infeld and van der Waerden, but it is in fact developed quite independently of this.) Owing to the fact that all general relations had earlier already been written in a generally covariant form they may be taken over unchanged into the present context. In particular,

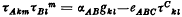
now serves as a defining relation for the connecting quantities τAkl. A linear rotor connection is introduced, and the covariant derivative of a rotor defined. The covariant constancy of the τAkl establishes the relation between the linear connections in w-space and in r-space. A rotor curvature tensor is considered alongside a number of other curvature objects. Next, conformal transformations are dealt with, of which duality rotations may be considered as a special case. This leads naturally to a gauge-covariant generalization of the whole calculus. A so-called rotor-derivative is defined, and some general relations involving such derivatives investigated. The relation of the rotor curvature tensor to the spin-curvature tensor is touched upon, after which the introduction of “geodesic frames” is considered. After this general theory some points concerning the Maxwell field are dealt with, which is followed by some work concerning basic quadratic and cubic invariants. Finally, a certain basic symmetric rotor is re-considered in the context of the classification of Weyl tensors, and the idea of a canonical representation suggested.