Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-22T17:56:58.608Z Has data issue: false hasContentIssue false
  • English
  • Français

On recursive solutions of a unit fraction equation

Part of: Computational number theory Diophantine equations Sequences and sets Multiplicative number theory

Published online by Cambridge University Press:  09 April 2009

Lawrence Brenton  and
Robert R. Bruner
Lawrence Brenton
Affiliation:
Wayne State University, Detroit, Michigan 48202, U.S.A., [email protected]
Robert R. Bruner
Affiliation:
Wayne State University, Detroit, Michigan 48202, U.S.A., [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

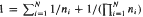We consider the Egyptian fraction equation and discuss techniques for generating solutions. By examining a quadratic recurrence relation modulo a family of primes we have found some 500 new infinite sequences of solutions. We also initiate an investigation of the randomness of the distribution of solutions, and show that there are infinitely many solutions not generated by the aforementioned technique.

MSC classification

Secondary: 11D68: Rational numbers as sums of fractions 11N45: Asymptotic results on counting functions for algebraic and topological structures 11B50: Sequences (mod $m$) 11Y50: Computer solution of Diophantine equations
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 57 , Issue 3 , December 1994 , pp. 341 - 356
Copyright
Copyright © Australian Mathematical Society 1994

References

[1]Barbeau, E., ‘Expressing one as a sum of distinct reciprocals: comments and a bibliography’, Eureka(Crux Math.) 3 (1977), 178–181.Google Scholar
[2]Brenton, L. and Hill, R., ‘On the diophantine equation and a class of homologically trivial complex surface singularities’, Pacific J. Math. 133 (1988), 41–67.Google Scholar
[3]Burshtein, N., ‘On distinct unit fractions whose sum equals 1’, Discrete Math. 5 (1973), 201–206.Google Scholar
[4]Cao, Z., Liu, R. and Zhang, L., ‘On the equation and Znám's problem’, J. Number Theory 27 (1987), 206–211.Google Scholar
[5]Curtiss, D., ‘On Kellogg's diophantine problem’, Amer. Math. Monthly 29 (1922), 380–387.CrossRefGoogle Scholar
[6]Grauert, H., ‘Über modifikationen und exzeptionelle analytische Mengen’, Math. Ann. 146 (1962), 331–368.Google Scholar
[7]Johannessen, D. M. and Søhus, T. V., ‘On stambrøker’, Nord. Mat. Tidskr. 22 (1974), 103–107.Google Scholar
[8]Knuth, D., The art of computer programming, volume 2 (Addison-Wesley, Reading, 1968).Google Scholar
[9]Sun, Q., ‘On a problem of Znám’, Sichuan Daxue Xuebao 4 (1983), 9–11.Google Scholar
[10]Sylvester, J., ‘On a point in the theory of vulgar fractions’, Amer. J. Math. 3 (1880), 332–335, 388–389.Google Scholar