Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-23T04:27:06.911Z Has data issue: false hasContentIssue false
  • English
  • Français

ON MODULES OVER COMMUTATIVE RINGS

Part of: Theory of modules and ideals

Published online by Cambridge University Press:  21 November 2017

LÁSZLÓ FUCHS  and
SANG BUM LEE
LÁSZLÓ FUCHS
Affiliation:
Department of Mathematics, Tulane University, New Orleans, Louisiana 70118, USA email [email protected]
SANG BUM LEE*
Affiliation:
Department of Mathematics, Sangmyung University, Seoul 110-743, Korea email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Our main purpose is to extend several results of interest that have been proved for modules over integral domains to modules over arbitrary commutative rings 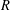$R$ with identity. The classical ring of quotients 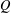$Q$ of 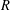$R$ will play the role of the field of quotients when zero-divisors are present. After discussing torsion-freeness and divisibility (Sections 2–3), we study Matlis-cotorsion modules and their roles in two category equivalences (Sections 4–5). These equivalences are established via the same functors as in the domain case, but instead of injective direct sums 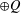$\oplus Q$ one has to take the full subcategory of 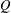$Q$-modules into consideration. Finally, we prove results on Matlis rings, i.e. on rings for which 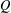$Q$ has projective dimension 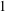$1$ (Theorem 6.4).

Keywords

Commutative ringstorsion-freetorsiondivisible and h-divisible modulescotorsion modulesgeneralized Matlis category equivalencetight systemMatlis rings

MSC classification

Primary: 13C13: Other special types
Secondary: 13C11: Injective and flat modules and ideals
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 103 , Issue 3 , December 2017 , pp. 341 - 356
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

References

Angeleri Hügel, L., Herbera, D. and Trlifaj, J., ‘Divisible modules and localization’, J. Algebra 294 (2005), 519–551.Google Scholar
Bass, H., ‘Finitistic dimension and a homological characterization of semiprimary rings’, Trans. Amer. Math. Soc. 95 (1960), 466–488.Google Scholar
Bazzoni, S., Eklof, P. C. and Trlifaj, J., ‘Tilting cotorsion pairs’, Bull. Lond. Math. Soc. 37 (2005), 683–696.Google Scholar
Bazzoni, S. and Herbera, D., ‘Cotorsion pairs generated by modules of bounded projective dimension’, Israel J. Math. 174 (2009), 119–160.CrossRefGoogle Scholar
Bican, L., El Bashir, R. and Enochs, E., ‘All modules have flat covers’, Bull. Lond. Math. Soc. 33 (2001), 385–390.Google Scholar
Cartan, H. and Eilenberg, S., Homological Algebra (Princeton University Press, Princeton, NJ, 1956).Google Scholar
Dauns, J. and Fuchs, L., ‘Torsion-freeness for rings with zero-divisors’, J. Algebra Appl. 3 (2004), 221–237.CrossRefGoogle Scholar
Fuchs, L., ‘Cotorsion and Tor pairs and finitistic dimensions over commutative rings’, in: Groups, Modules, and Model Theory—Surveys and Recent Developments (Springer, Cham, 2017), 317–330.CrossRefGoogle Scholar
Fuchs, L. and Lee, S. B., ‘The functor Hom and cotorsion theories’, Comm. Algebra 37 (2009), 923–932.CrossRefGoogle Scholar
Fuchs, L. and Salce, L., Modules over Non-Noetherian Domains, Mathematical Surveys and Monographs, 84 (American Mathematical Society, Providence, RI, 2001).Google Scholar
Göbel, R. and Trlifaj, J., Approximations and Endomorphism Algebras of Modules, Expositions in Mathematics, 41 (Walter de Gruyter, Berlin, 2006).Google Scholar
Hamsher, R. M., ‘On the structure of a one-dimensional quotient field’, J. Algebra 19 (1971), 416–425.CrossRefGoogle Scholar
Harrison, D. K., ‘Infinite abelian groups and homological methods’, Ann. of Math. (2) 69 (1959), 366–391.CrossRefGoogle Scholar
Lee, S. B., ‘On divisible modules over domains’, Arch. Math. 53 (1989), 259–262.Google Scholar
Lee, S. B., ‘Weak-injective modules’, Comm. Algebra 34 (2006), 361–370.CrossRefGoogle Scholar
Lee, S. B., ‘Modules over AW domains’, Preprint.Google Scholar
Matlis, E., ‘Divisible modules’, Proc. Amer. Math. Soc. 11 (1960), 385–391.Google Scholar
Matlis, E., ‘Cotorsion modules’, Mem. Amer. Math. Soc. 49 (1964).Google Scholar
Matlis, E., 1-Dimensional Cohen-Macaulay Rings, Lecture Notes in Mathematics, 327 (Springer, Berlin, 1973).CrossRefGoogle Scholar
Stenström, B., Rings of Quotients, Grundlehren der Mathematischen Wissenschaften, 217 (Springer, New York, 1975).Google Scholar