Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Weichsel, Paul M.
1967.
On metabelian p-groups.
Journal of the Australian Mathematical Society,
Vol. 7,
Issue. 1,
p.
55.
Brisley, Warren
1967.
On varieties of metabelian p-groups, and their laws.
Journal of the Australian Mathematical Society,
Vol. 7,
Issue. 1,
p.
64.
Brisley, Warren
and
Macdonald, I. D.
1969.
Two classes of metabelianp-groups.
Mathematische Zeitschrift,
Vol. 112,
Issue. 1,
p.
5.
Kovács, L. G.
and
Newman, M. F.
1971.
On non-cross varieties of groups.
Journal of the Australian Mathematical Society,
Vol. 12,
Issue. 2,
p.
129.
Brisley, Warren
and
Kovács, L.G.
1971.
On soluble groups of prime-power exponent.
Bulletin of the Australian Mathematical Society,
Vol. 4,
Issue. 3,
p.
389.
Macdonald, I. D.
1971.
Solution of the Hughes problem for finite 𝑝-groups of class 2𝑝-2..
Proceedings of the American Mathematical Society,
Vol. 27,
Issue. 1,
p.
39.
Brisley, Warren
1971.
Varieties of Metabelian p-Groups of Class b, p+1.
Journal of the Australian Mathematical Society,
Vol. 12,
Issue. 1,
p.
53.
Plotkin, B. I.
1973.
General theory of groups.
Journal of Soviet Mathematics,
Vol. 1,
Issue. 5,
p.
527.
Chunikhin, S. A.
and
Shemetkov, L. A.
1973.
Finite groups.
Journal of Soviet Mathematics,
Vol. 1,
Issue. 3,
p.
291.
Groves, J. R. J.
1974.
Regular groups in varieties ofp-groups.
Israel Journal of Mathematics,
Vol. 19,
Issue. 4,
p.
382.
Thomson, Michael W.
1977.
Subgroups of finitely presented solvable linear groups.
Transactions of the American Mathematical Society,
Vol. 231,
Issue. 1,
p.
133.
Miller, Jay I.
1979.
Just non-metabelian groups.
Mathematische Zeitschrift,
Vol. 166,
Issue. 1,
p.
1.
Meixner, Thomas
1981.
Power automorphisms of finitep-groups.
Israel Journal of Mathematics,
Vol. 38,
Issue. 4,
p.
345.
Kappe, Luise-Charlotte
1983.
Engel margins in metabelian groups.
Communications in Algebra,
Vol. 11,
Issue. 17,
p.
1965.
Fitzpatrick, Patrick
and
Kovács, L. G.
1983.
Varieties of nilpotent groups of class four (I).
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 35,
Issue. 1,
p.
59.
Bryce, R. A.
Cossey, John
and
Ormerod, E. A.
1992.
A note on p-groups with power automorphisms.
Glasgow Mathematical Journal,
Vol. 34,
Issue. 3,
p.
327.
Newman, M.F.
and
Xu, Ming-Yao
1992.
A note on regular metabelian groups of prime-power order.
Bulletin of the Australian Mathematical Society,
Vol. 46,
Issue. 2,
p.
343.
Traustason, Gunnar
1998.
On groups in which every subgroup is subnormal of defect at most three.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 64,
Issue. 3,
p.
397.
Ormerod, Elizabeth A.
1999.
A note on the wielandt subgroup of a metabelianp-group.
Communications in Algebra,
Vol. 27,
Issue. 2,
p.
621.
Traustason, Gunnar
2000.
On 3-Baer groups.
Journal of Group Theory,
Vol. 3,
Issue. 3,
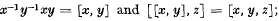 further [x, 0y] = x and [x, ky] = [x, (k—1)y, y] for all positive integers k. The s-th term γs(G) of the lower central series of a group G is the subgroup of G generated by [a1, … as] for all a1, … as, in G. A group G is metabelian if [[a11, a2], [a3, a4]] = e (the identity element) for all a1, a2, a3, a4, in G, and has exponent k if ak = e for all a in G.
further [x, 0y] = x and [x, ky] = [x, (k—1)y, y] for all positive integers k. The s-th term γs(G) of the lower central series of a group G is the subgroup of G generated by [a1, … as] for all a1, … as, in G. A group G is metabelian if [[a11, a2], [a3, a4]] = e (the identity element) for all a1, a2, a3, a4, in G, and has exponent k if ak = e for all a in G.

