Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T12:01:00.429Z Has data issue: false hasContentIssue false
  • English
  • Français

ON INTEGERS OCCURRING AS THE MAPPING DEGREE BETWEEN QUASITORIC 4-MANIFOLDS

Part of: Classical Topics in Algebraic Topology Complex manifolds Operations and obstructions

Published online by Cambridge University Press:  23 December 2016

ÐORÐE B. BARALIĆ
ÐORÐE B. BARALIĆ*
Affiliation:
Mathematical Institute SASA, Kneza Mihaila 36, p.p. 367, 11001 Belgrade, Serbia email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the set 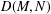$D(M,N)$ of all possible mapping degrees from 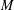$M$ to 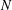$N$ when 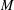$M$ and 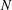$N$ are quasitoric 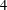$4$-manifolds. In some of the cases, we completely describe this set. Our results rely on Theorems proved by Duan and Wang and the sets of integers obtained are interesting from the number theoretical point of view, for example those representable as the sum of two squares 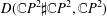$D(\mathbb{C}P^{2}\sharp \mathbb{C}P^{2},\mathbb{C}P^{2})$ or the sum of three squares 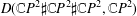$D(\mathbb{C}P^{2}\sharp \mathbb{C}P^{2}\sharp \mathbb{C}P^{2},\mathbb{C}P^{2})$. In addition to the general results about the mapping degrees between quasitoric 4-manifolds, we establish connections between Duan and Wang’s approach, quadratic forms, number theory and lattices.

Keywords

mapping degreequasitoric manifoldsquadratic formsintersection form

MSC classification

Primary: 55M25: Degree, winding number
Secondary: 55S37: Classification of mappings 32Q55: Topological aspects of complex manifolds
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 103 , Issue 3 , December 2017 , pp. 289 - 312
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Agaian, S. S., Hadamard Matrices and Their Applications, Lecture Notes in Mathematics, 1168 (Springer, Berlin–Heidelberg, 1985).CrossRefGoogle Scholar
Baues, H. J., ‘The degree of maps between certain 6-manifolds’, Compositio Math. 110 (1998), 51–64.Google Scholar
Berstein, I. and Edmonds, A. L., ‘On the construction of branched coverings of low-dimensional manifolds’, Trans. Amer. Math. Soc. 247 (1979), 87–124.Google Scholar
Bredon, G., Topology and Geometry, Graduate Texts in Mathematics, 139 (Springer, New York, 1993).CrossRefGoogle Scholar
Buchstaber, V. and Panov, T., Torus Actions and their Applications in Topology and Combinatorics, AMS University Lecture Series, 24 (American Mathematical Society, Providence, RI, 2002).Google Scholar
Bullen, P. S., A Dictionary of Inequalities (Chapman & Hall, Boca Raton, FL, 1998).Google Scholar
Burton, D. M., Elementary Number Theory, 7th edn (McGraw-Hill, New York, 2007).Google Scholar
Conway, J. H., The Sensual (Quadratic) Form, The Carus Mathematical Monographs, 26 (Mathematical Association of America, Washington, DC, 1997).Google Scholar
Davis, M. and Januszkiewicz, T., ‘Convex polytopes, Coxeter orbifolds and torus actions’, Duke Math. J. 62(2) (1991), 417–451.Google Scholar
Duan, H., ‘Self-maps on the Grassmannian of complex structure’, Compositio Math. 132 (2002), 159–175.Google Scholar
Duan, H. and Wang, S., ‘The degrees of maps between manifolds’, Math. Z. 244(1) (2003), 67–89.Google Scholar
Duan, H. and Wang, S., ‘Non-zero degree maps between 2n-manifolds’, Acta Math. Sin. (Engl. Ser.) 20(1) (2004), 1–14.CrossRefGoogle Scholar
Edmonds, A. L., ‘Deformation of maps to branched coverings in dimension two’, Ann. of Math. (2) 110(1) (1979), 113–125.CrossRefGoogle Scholar
Feder, S. and Gitler, S., ‘Mappings of quaternionic projective space’, Bol. Soc. Mat. Mexicana (3) 18 (1973), 33–37.Google Scholar
Gauss, C. F., Disquisitiones Arithmeticae (Leipzig, Fleischer, 1801).Google Scholar
Hatcher, A., Algebraic Topology, 1st edn (Cambridge University Press, Cambridge, 2001).Google Scholar
Hayat-Legrand, C., Matveev, S. and Zieschang, H., ‘Computer calculation of the degree of maps into the Poincaré homology sphere’, Exp. Math. 10 (2001), 497–508.Google Scholar
Hirzebruch, F., ‘Über eine Klasse von einfachzusammenhängenden komplexen Manningfaltigkeiten’, Math. Ann. 124 (1951), 77–86 (in German).Google Scholar
Kneser, H., ‘Glätung von Flächenabbildugen’, Math. Ann. 100 (1928), 609–617 (in German).Google Scholar
Kreck, M. and Crowley, D., ‘Hirzebruch surfaces’, Bull. Manifold Atlas (2011), 19–22.Google Scholar
Legendre, A. M., Essai sur la théorie des nombres (Duprat, Paris, 1798), An VI, pp. 202, 398–399.Google Scholar
Milnor, J. and Husemoller, D., Symmetric Billinear Forms, Ergebnisse der Mathematik und ihrer Grenzgebiete. 2. Folge, 73 (Springer, Berlin–Heidelberg, 1973).CrossRefGoogle Scholar
Nathanson, M. B., Elementary Methods in Number Theory, Graduate Texts in Mathematics, 195 (Springer, New York, 1991).Google Scholar
Orlik, P. and Raymond, F., ‘Actions of the torus on 4-manifolds’, Trans. Amer. Math. Soc. 152 (1970), 531–559.Google Scholar
Paley, R. E. A. C., ‘On orthogonal matrices’, J. Math. Phys. 12 (1933), 311–320.Google Scholar
Sankaran, P. and Sarkar, S., ‘Degrees of maps between Grassmann manifolds’, Osaka J. Math. 46(4) (2009), 1143–1161.Google Scholar
Wang, S., ‘Non-zero degree maps between 3-manifolds’, in: Proc. ICM 2002 II, Beijing, China, 20–28 August 2002 (ed. Li, T. D.) (Higher Education Press, Beijing, 2002), 457–470.Google Scholar