Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dung, Nguyen Viet
1997.
On indecomposable decompositions of CS-modules II.
Journal of Pure and Applied Algebra,
Vol. 119,
Issue. 2,
p.
139.
Dung, Nguyen Viet
1997.
Modules with Indecomposable Decompositions That Complement Maximal Direct Summands.
Journal of Algebra,
Vol. 197,
Issue. 2,
p.
449.
Santa-Clara, Catarina
1998.
Extending modules with injective or semisimple summands.
Journal of Pure and Applied Algebra,
Vol. 127,
Issue. 2,
p.
193.
Dogruöz, Semra
and
Smith, Patrick F.
1998.
Modules which are extending relative to module classes.
Communications in Algebra,
Vol. 26,
Issue. 6,
p.
1699.
Gómez Pardo, José
and
Guil Asensio, Pedro
2000.
Every Σ-CS-module has an indecomposable decomposition.
Proceedings of the American Mathematical Society,
Vol. 129,
Issue. 4,
p.
947.
Er, Noyan
2004.
Artinian Rings Characterized by Direct Sums of CS Modules.
Communications in Algebra,
Vol. 32,
Issue. 12,
p.
4821.


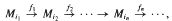 , with distinct
, with distinct 