Hostname: page-component-5cf477f64f-bmd9x Total loading time: 0 Render date: 2025-04-02T23:47:43.026Z Has data issue: false hasContentIssue false
  • English
  • Français

ON GENERALIZED THUE–MORSE FUNCTIONS AND THEIR VALUES

Part of: Algebraic number theory: global fields Diophantine approximation, transcendental number theory

Published online by Cambridge University Press:  11 March 2019

DZMITRY BADZIAHIN Open the ORCID record for DZMITRY BADZIAHIN [Opens in a new window]  and
EVGENIY ZORIN Open the ORCID record for EVGENIY ZORIN [Opens in a new window]
DZMITRY BADZIAHIN
Affiliation:
Department of Mathematical Sciences, Durham University, Lower Mountjoy, Stockton Road, Durham DH1 3LE, UK email [email protected]
EVGENIY ZORIN*
Affiliation:
The University of York, Department of Mathematics, Heslington, York YO10 5DD, UK email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we extend and generalize, up to a natural bound of the method, our previous work Badziahin and Zorin [‘Thue–Morse constant is not badly approximable’, Int. Math. Res. Not. IMRN 19 (2015), 9618–9637] where we proved, among other things, that the Thue–Morse constant is not badly approximable. Here we consider Laurent series defined with infinite products 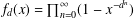$f_{d}(x)=\prod _{n=0}^{\infty }(1-x^{-d^{n}})$, 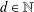$d\in \mathbb{N}$, 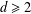$d\geq 2$, which generalize the generating function 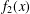$f_{2}(x)$ of the Thue–Morse number, and study their continued fraction expansion. In particular, we show that the convergents of 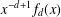$x^{-d+1}f_{d}(x)$ have a regular structure. We also address the question of whether the corresponding Mahler numbers 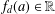$f_{d}(a)\in \mathbb{R}$, 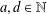$a,d\in \mathbb{N}$, 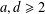$a,d\geq 2$, are badly approximable.

Keywords

diophantine approximationsMahler numbersThue–Morseautomatic numberscontinued fractions

MSC classification

Secondary: 11R06: PV-numbers and generalizations; other special algebraic numbers; Mahler measure 11J70: Continued fractions and generalizations
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 108 , Issue 2 , April 2020 , pp. 177 - 201
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

Footnotes

Dzmitry Badziahin acknowledges the support of EPSRC Grant EP/E061613/1. Evgeniy Zorin acknowledges the support of EPSRC Grant EP/M021858/1.

References

Allouche, J. P., Mendès France, M. and van der Poorten, A. J., ‘An infinite product with bounded partial quotients’, Acta Arith. 59 (1991), 171–182.Google Scholar
Badziahin, D. A. and Zorin, E., ‘Thue–Morse constant is not badly approximable’, Int. Math. Res. Not. IMRN 19 (2015), 9618–9637.Google Scholar
Bugeaud, Y., ‘On the irrationality exponent of the Thue–Morse–Mahler numbers’, Ann. Inst. Fourier (Grenoble) 61(5) (2011), 2065–2076.Google Scholar
Bugeaud, Y., Han, G.-N., Wen, Z.-Y. and Yao, J.-Y., ‘Hankel determinants, Padé approximations, and irrationality exponents’, Int. Math. Res. Not. IMRN 5 (2016), 1467–1496.Google Scholar
Mendès France, M. and van der Poorten, A. J., ‘From geometry to Euler identities’, Theoret. Comput. Sci. 65(2) (1989), 213–220.Google Scholar
Mendès France, M. and van der Poorten, A. J., ‘Some explicit continued fraction expansions’, Mathematika 38(1) (1991), 1–9.Google Scholar
Montgomery, P. L., ‘New solutions of a p-1 ≡ 1 mod p 2’, Math. Comp. 61 (1993), 361–363.Google Scholar
van der Poorten, A. J., ‘Formal power series and their continued fraction expansion’, in: Algorithmic Number Theory (Proc. Third International Symposium, ANTS-III, Portland, Oregon, June 1998), Springer Lecture Notes in Computer Science, 1423 (1998), 358–371.Google Scholar
Ribenboim, P., Die Welt der Primzahlen: Geheimnisse und Rekorde (Springer, New York, 2004), 237 (in German).Google Scholar