Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-28T16:00:55.977Z Has data issue: false hasContentIssue false
  • English
  • Français

On functions of bounded variation relative to a set

Published online by Cambridge University Press:  09 April 2009

P. C. Bhakta
P. C. Bhakta
Affiliation:
Department of Mathematics Jadavpur UniversityCalcutta-32, India
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The present paper on functions of bounded variation relative to a set has its point of departure in the work of R. L. Jeffery [10]. Below we recapitulate Jeffery's class U of functions of bounded variation relative to a set, we state and prove a number of preliminary lemmas and theorems, we introduce a suitable pseudo- metric space (X, d) of such functions, and the analogous space 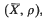, and prove that (X, d) is separable, that every closed sphere in (X, d) is compact and that 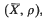is complete. These results extend known results of C. R. Adams, and C. R. Adams and A. P. Morse for the space of usual BV functions.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 13 , Issue 3 , May 1972 , pp. 313 - 322
Copyright
Copyright © Australian Mathematical Society 1972

References

[1]Adams, C. R., ‘The space of functions of bounded variation and certain general spaces’, Trans. Amer. Math. Soc., 40 (1936), 421–438.CrossRefGoogle Scholar
[2]Adams, C. R. and Clarkson, J. A., ‘On convergence in Variation’, Bull. Amer. Math. Soc., 40 (1934), 413–417.CrossRefGoogle Scholar
[3]Adams, C. R. and Lewy, H., ‘On convergence in length’, Duke Math. Journal 1 (1935), 19–26.CrossRefGoogle Scholar
[4]Adams, C. R. and Morse, A. P., ‘On the space (BV)’, Trans. Amer. Math. Soc. 42 (1937), 194–205.Google Scholar
[5]Cesari, L., ‘Sulle funzioni a Variazione limitata’, Annali R. Scoula Normale Sup. Pisa, Series II, 5 (1936).Google Scholar
[6]Cesari, L., ‘Funzioni continue a variazine limitata in Un insieme’, Mem. Accad. Sci. 1st. Bologna, cl. Sci. Fis (10) 2 (1946), 127–145.Google Scholar
[7]Cesari, L., ‘Invertibilita in piccolo delle funzioni continue e teorema di derivazione’, Mem. Accad. Sci. 1st. Bologna cl. Sci. Fis (10) 3 (1947), 99–112.Google Scholar
[8]Cesari, L., ‘Sul teorema di derivazione dulle funzioni variazione limitata in Un insieme’, Mem. Accad. Sci. 1st. Bologna cl. Sci. Fis (10) 8 (1950—1951), 223–229.Google Scholar
[9]Cesari, L., ‘Variation, multiplicity and semi-continuity’, Amer. Math. Monthly 65 (1958), 317–332.CrossRefGoogle Scholar
[10]Jeffery, R. L., ‘Generalised integrals with respect to functions of bounded variation’, Can. J. Math. 10 (1958), 617–628.CrossRefGoogle Scholar
[11]Krickeberg, K., ‘Distributionen functionen beschrankter variation und Lebesguescher inhalt nichtparamätrischer flachen’, Annali Matem. Pura appl. (4) 44 (1957), 105–133.CrossRefGoogle Scholar
[12]Kelley, J. H., General Topology (Van Nostrand, New York, 1955).Google Scholar
[13]Natanson, I. P., Theory of functions of a real variable. Vol. I, (Unger, New York, 1960).Google Scholar
[14]Saks, S., Theory of the integral (Warsaw, 1937; Dover, New York, 1964).Google Scholar