No CrossRef data available.
Article contents
On Fourier transform multipliers in Lp
Published online by Cambridge University Press: 09 April 2009
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We denote by R the set of real numbers, and by Rn, n ≧ 2, the Euclidean space of dimension n. Given any subset E of Rn, n ≧ 1, we denote the characteristic function of E by xE, so that XE(x) = 0 if x ∈ E; and XE(X) = 0 if x ∈ Rn/E.The space L(Rn) Lp consists of those measurable functions f on Rn such that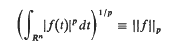 
is finite. Also, L∞ represents the space of essentially bounded measurable functions with ║f║>0; m({x: |f(x)| > x}) = O}, where m represents the Lebesgue measure on Rn The numbers p and p′ will be connected by l/p+ l/p′= 1.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1972
References
[1]Brainerd, B. and Edwards, R. E., ‘Linear operators which commute with translations’, J. Austral. Math. Soc. 6 (1966) 289–327, 328–350.CrossRefGoogle Scholar
[2]Hörmander, L., ‘Estimates for translation invariant operators in Lp spaces’, Acta Math. 104 (1960), 93–140.CrossRefGoogle Scholar
[4]Littman, W., ‘Multipliers in Lp and interpolation’ Bull. Amer. Math. Soc., 71 (1965), 764–766.CrossRefGoogle Scholar
[5]Littman, W., McCarthy, C. and Riviere, N., ‘Lp-multiplier theorems’, Studia Math. 30 (1968), 193–217.CrossRefGoogle Scholar
[6]Mihlin, S. G., ‘On the multipliers of Fourier integrals’, Dokl. Akad. Nauk SSSR (N.S.) 109 (1956), 701–703.Google Scholar
[7]Stein, E. M., ‘On limits of sequences of operators’, Ann. of Math. 74 (1961), 140–170.CrossRefGoogle Scholar
[8]Titchmarsh, E. C., Introduction to the theory of Fourier integrals, (Oxford, 1937).Google Scholar
[10]Okikiolu, G. O., ‘On the theory and applications of Dirichlet projections’, J. für die reine angew. Math. 245 (1970), 149–164.Google Scholar
You have
Access