Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T14:26:43.223Z Has data issue: false hasContentIssue false
  • English
  • Français

ON DIFFERENTIAL CHARACTERISTIC CLASSES

Part of: Differential topology Topological $K$-theory Global differential geometry

Published online by Cambridge University Press:  04 December 2014

MAN-HO HO
MAN-HO HO*
Affiliation:
Department of Mathematics, Hong Kong Baptist University, Kowloon Tong, Kowloon, Hong Kong email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we give explicit formulas for differential characteristic classes of principal 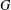$G$-bundles with connections and prove their expected properties. In particular, we obtain explicit formulas for differential Chern classes, differential Pontryagin classes and the differential Euler class. Furthermore, we show that the differential Chern class is the unique natural transformation from (Simons–Sullivan) differential 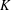$K$-theory to (Cheeger–Simons) differential characters that is compatible with curvature and characteristic class. We also give the explicit formula for the differential Chern class on Freed–Lott differential 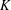$K$-theory. Finally, we discuss the odd differential Chern classes.

Keywords

characteristic classesdifferential charactersdifferential K-theory

MSC classification

Primary: 53C08: Gerbes, differential characters
Secondary: 57R20: Characteristic classes and numbers 19L50: Twisted $K$-theory; differential $K$-theory
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 99 , Issue 1 , August 2015 , pp. 30 - 47
Copyright
© 2014 Australian Mathematical Publishing Association Inc. 

References

Bär, C. and Becker, C., ‘Differential characters and geometric chains’, in: Differential Characters, Lecture Notes in Mathematics, 2112 (Springer International Publishing, Cham, 2014), 1–187.CrossRefGoogle Scholar
Berthomieu, A., ‘A version of smooth K-theory adapted to the total Chern class’, J. K-Theory 6(2) (2010), 197–230.CrossRefGoogle Scholar
Brylinski, J.-L., Loop Spaces, Characteristic Classes and Geometric Quantization, Modern Birkhäuser Classics (Birkhäuser, Boston, 2008), reprint of the 1993 edition.Google Scholar
Bunke, U., ‘Chern classes on differential K-theory’, Pacific J. Math. 247(2) (2010), 313–322.CrossRefGoogle Scholar
Bunke, U. and Schick, T., ‘Smooth K-theory’, Astérisque 328 (2009), 45–135.Google Scholar
Bunke, U. and Schick, T., ‘Uniqueness of smooth extensions of generalized cohomology theories’, J. Topol. 3 (2010), 110–156.CrossRefGoogle Scholar
Cheeger, J. and Simons, J., ‘Differential characters and geometric invariants’, in: Geometry and Topology (College Park, MD 1983/84), Lecture Notes in Mathematics, 1167 (eds. Alexander, J. and Harer, J.) (Springer, Berlin, 1985), 50–80.Google Scholar
Chern, S.-S. and Simons, J., ‘Characteristic forms and geometric invariants’, Ann. of Math. (2) 99 (1974), 48–69.CrossRefGoogle Scholar
Dupont, J., Hain, R. and Zucker, S., ‘Regulators and characteristic classes of flat bundles’, in: The Arithmetic and Geometry of Algebraic Cycles (Banff, AB, 1998), CRM Proceedings & Lecture Notes, 24 (American Mathematical Society, Providence, RI, 2000), 47–92.Google Scholar
Freed, D. and Lott, J., ‘An index theorem in differential K-theory’, Geom. Topol. 14 (2010), 903–966.CrossRefGoogle Scholar
Hekmati, P., Murray, M. K., Schlegel, V. S. and Vozzo, R. F., ‘A geometric model for odd differential $K$-theory’. arXiv:1309.2834.Google Scholar
Ho, M.-H., ‘The differential analytic index in Simons-Sullivan differential K-theory’, Ann. Global Anal. Geom. 42(4) (2012), 523–535.CrossRefGoogle Scholar
Ho, M.-H., ‘Remarks on flat and differential K-theory’, Ann. Math. Blaise Pascal 21(1) (2014), 91–101.CrossRefGoogle Scholar
Hopkins, M. and Singer, I. M., ‘Quadratic functions in geometry, topology, and M-theory’, J. Differential Geom. 70 (2005), 329–425.CrossRefGoogle Scholar
Klonoff, K., ‘An index theorem in differential $K$-theory’, PhD Thesis, The University of Texas at Austin, ProQuest LLC, Ann Arbor, MI, 2008.Google Scholar
Kreck, M., Differential Algebraic Topology, Graduate Studies in Mathematics, 110 (American Mathematical Society, Providence, RI, 2010).CrossRefGoogle Scholar
Mead, D. G., ‘Newton’s identities’, Amer. Math. Monthly 99(8) (1992), 749–751.CrossRefGoogle Scholar
Pingali, V. P. and Takhtajan, L. A., ‘On Bott–Chern forms and their applications’, Math. Ann. 360(1–2) (2014), 519–546.CrossRefGoogle Scholar
Simons, J. and Sullivan, D., ‘Structured vector bundles define differential K-theory’, in: Quanta of Maths, Clay Mathematics Proceedings, 11 (American Mathematical Society, Providence, RI, 2010), 579–599.Google Scholar
Tradler, T., Wilson, S. O. and Zeinalian, M., ‘An elementary differential extension of odd K-theory’, J. K-Theory 12(2) (2013), 331–361.CrossRefGoogle Scholar