Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Neuhauser, Markus
2003.
Kazhdan constants for conjugacy classes of compact groups.
Journal of Algebra,
Vol. 270,
Issue. 2,
p.
564.
Neuhauser, Markus
2006.
Kazhdan constants for compact groups.
Journal of the Australian Mathematical Society,
Vol. 81,
Issue. 1,
p.
11.


 if
if 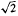 if
if 