Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chaki, M. C.
and
Ghosh, D.
1972.
On a type of Sasakian space.
Journal of the Australian Mathematical Society,
Vol. 13,
Issue. 4,
p.
508.
Kaigorodov, V. R.
1985.
Structure of space-time curvature.
Journal of Soviet Mathematics,
Vol. 28,
Issue. 2,
p.
256.
Senovilla, José M M
2008.
Second-order symmetric Lorentzian manifolds: I. Characterization and general results.
Classical and Quantum Gravity,
Vol. 25,
Issue. 24,
p.
245011.
Kim, Jaeman
2014.
ON W4-BIRECURRENT MANIFOLDS.
Honam Mathematical Journal,
Vol. 36,
Issue. 4,
p.
723.


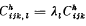 where
where 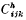 is the conformal curvature tensor:
is the conformal curvature tensor: