Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Embrechts, Paul
and
Goldie, Charles M.
1982.
On convolution tails.
Stochastic Processes and their Applications,
Vol. 13,
Issue. 3,
p.
263.
Embrechts, Paul
and
Omey, Edward
1984.
A property of longtailed distributions.
Journal of Applied Probability,
Vol. 21,
Issue. 1,
p.
80.
Davis, Richard
and
Resnick, Sidney
1985.
More limit theory for the sample correlation function of moving averages.
Stochastic Processes and their Applications,
Vol. 20,
Issue. 2,
p.
257.
Davis, Richard
and
Resnick, Sidney
1986.
Dependence in Probability and Statistics.
p.
417.
Resnick, Sidney I.
1986.
Point processes, regular variation and weak convergence.
Advances in Applied Probability,
Vol. 18,
Issue. 1,
p.
66.
Cline, Daren B. H.
1986.
Convolution tails, product tails and domains of attraction.
Probability Theory and Related Fields,
Vol. 72,
Issue. 4,
p.
529.
Omey, E.
and
Willekens, E.
1987.
Stability Problems for Stochastic Models.
Vol. 1233,
Issue. ,
p.
103.
Cline, Daren B. H.
1987.
Convolutions of Distributions With Exponential and Subexponential Tails.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 43,
Issue. 3,
p.
347.
Omey, E.
and
Willekens, E.
1987.
Theory prob. appl..
Communications in Statistics. Stochastic Models,
Vol. 3,
Issue. 3,
p.
311.
Goldie, Charles M.
and
Sidney, Resnick
1988.
Subexponential distribution tails and point processes.
Communications in Statistics. Stochastic Models,
Vol. 4,
Issue. 2,
p.
361.
Klüppelberg, Claudia
1988.
Subexponential distributions and integrated tails.
Journal of Applied Probability,
Vol. 25,
Issue. 1,
p.
132.
Goldie, Charles M.
and
Resnick, Sidney
1988.
Distributions that are both subexponential and in the domain of attraction of an extreme-value distribution.
Advances in Applied Probability,
Vol. 20,
Issue. 4,
p.
706.
Cline, Daren B.H.
1989.
Consistency for least squares regression estimators with infinite variance data.
Journal of Statistical Planning and Inference,
Vol. 23,
Issue. 2,
p.
163.
Leslie, J. R.
1989.
On the non-closure under convolution of the subexponential family.
Journal of Applied Probability,
Vol. 26,
Issue. 1,
p.
58.
Murphree, Emily S.
1989.
Some new results on the subexponential class.
Journal of Applied Probability,
Vol. 26,
Issue. 04,
p.
892.
Murphree, Emily S.
1989.
Some new results on the subexponential class.
Journal of Applied Probability,
Vol. 26,
Issue. 4,
p.
892.
Cline, Daren B. H.
1990.
Convolutions of distrbutions with exponential and subexponential tails: Corrigendum.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 48,
Issue. 1,
p.
152.
Klüppelberg, Claudia
1990.
Asymptotic ordering of distribution functions and convolution semigroups.
Semigroup Forum,
Vol. 40,
Issue. 1,
p.
77.
Klüppelberg, Claudia
and
Villasenor, JoséA
1991.
The full solution of the convolution closure problem for convolution-equivalent distributions.
Journal of Mathematical Analysis and Applications,
Vol. 160,
Issue. 1,
p.
79.
Cline, Daren B.H.
and
Resnick, Sidney I.
1992.
Multivariate subexponential distributions.
Stochastic Processes and their Applications,
Vol. 42,
Issue. 1,
p.
49.
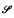 if {1 – F(2)(x)}/{1 – F(x)}→2 as x→∞, and F∈
if {1 – F(2)(x)}/{1 – F(x)}→2 as x→∞, and F∈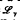 , if for some fixed γ > 0, and for each real
, if for some fixed γ > 0, and for each real 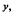 , limx→∞ {1 – F(x + y)}/{1 – F(x)} ═ e– n. Sufficient conditions are given for the statement F ∈
, limx→∞ {1 – F(x + y)}/{1 – F(x)} ═ e– n. Sufficient conditions are given for the statement F ∈ 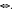 F * G ∈
F * G ∈ 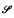 and when both F and G are in y it is proved that F*G∈
and when both F and G are in y it is proved that F*G∈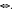 pF + 1(1 – p) G ∈ for some (all) p ∈(0,1). The related classes ℒt are proved closed under convolutions, which implies the closure of the class of positive random variables with regularly varying tails under multiplication (of random variables). An example is given that shows
pF + 1(1 – p) G ∈ for some (all) p ∈(0,1). The related classes ℒt are proved closed under convolutions, which implies the closure of the class of positive random variables with regularly varying tails under multiplication (of random variables). An example is given that shows 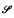 to be a proper subclass of ℒ 0.
to be a proper subclass of ℒ 0.