Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-24T02:23:45.836Z Has data issue: false hasContentIssue false
  • English
  • Français

On certain varieties of groups which are central extensions

Part of: Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  09 April 2009

R. A. Bryce
R. A. Bryce
Affiliation:
Department of Mathematics Faculty of Science Australian National UniversityP. O. Box 4 Canberra A. C. T. 2601, Australia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Connexions are sought between the subvarieties of a variety U of groups and the subvarieties of the variety 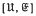of all groups which are central extensions by groups in U, in the case when U has the form 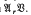. Here 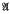, is the variety of abelian groups of exponent dividing r and Bis a variety of soluble groups of finite exponent.

MSC classification

Secondary: 20E10: Quasivarieties and varieties of groups
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 37 , Issue 3 , December 1984 , pp. 366 - 390
Copyright
Copyright © Australian Mathematical Society 1984

References

[1]Bryant, Roger M., ‘On s-critical groups’, Quart. J. Math. Oxford Ser. (2) 22 (1971), 91–101.CrossRefGoogle Scholar
[2]Bryant, Roger M., ‘Finite splitting groups in varieties of groups’, Quart. J. Math. Oxford Ser. (2) 22 (1971), 169–172.CrossRefGoogle Scholar
[3]Bryce, R. A., ‘Centre-by-abelian-by-nilpotent varieties of groups’, J. London Math. Soc. (2) 12 (1976), 337–350.CrossRefGoogle Scholar
[4]Greiss, Robert L. Jr, ‘Automorphisms of extra-special groups and non-vanishing degree 2 cohomology’, Pacific J. Math. 48 (1973), 403–422.CrossRefGoogle Scholar
[5]Huppert, B., Endliche Gruppen I (Springer-Verlag, Berlin-Heidelberg-New York, 1967).CrossRefGoogle Scholar
[6]Isaacs, I. Martin, ‘Primitive characters, normal subgroups, and M-groups’, Math. Z. 177 (1981), 267–284.CrossRefGoogle Scholar
[7]Kovács, L. G. and Newman, M. F., ‘On critical groups’, J. Austral. Math. Soc. 6 (1966), 237–250.CrossRefGoogle Scholar
[8]Neumann, B. H., ‘Groups with finite classes of conjugate elements’, Proc. London Math. Soc. (3) 1 (1951), 178–187.CrossRefGoogle Scholar
[9]Neumann, Hanna, Varieties of groups (Springer-Verlag, Berlin-Heidelberg-New York, 1967).CrossRefGoogle Scholar