Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-24T19:11:13.410Z Has data issue: false hasContentIssue false
  • English
  • Français

On certain direct sum decompositions of L1 spaces

Published online by Cambridge University Press:  09 April 2009

R. E. Edwards
R. E. Edwards
Affiliation:
Institute of Advanced Studies, A.N.U., Canberra.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let L1 denote temporarily the usual Lebesgue space over the circle group (equivalently: the additive group of real numbers modulo 2π), and let H1 denote the Hardy space comprised of those f in L1 whose complex Fourier coefficients vanish for all negative frequencies, so tha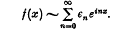 D. J. Newman has settled a conjecture by showing [1] that there exists no continuous projuction of L1 onto H1, i.e. that there exists in L1 no topological complement to H1.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 3 , Issue 2 , May 1963 , pp. 151 - 158
Copyright
Copyright © Australian Mathematical Society 1963

References

[1]Newman, D. J., The non-existence of projections from L1 to H1, Proc. Amer. Math. Soc. 12 (1961), 98–99.Google Scholar
[2]Zygmund, A., Trigonometric series, Vol. I, Cambridge University Press (1959).Google Scholar
[2′]Zygmund, A., Trigonometrical series, Warszawa-Lwow (1935).Google Scholar
[3]Weil, A., L'intégration dans les groupes topologiques et ses applications, Act. Sci. et Ind. Nc. 869–1145, Paris (1951).Google Scholar
[4]Hewitt, E. and Zuckerman, H. S., Some theorems on lacunary Fourier series, with extensions to compact groups, Trans. Amer. Math. Soc. 93 (1959). 1–19.CrossRefGoogle Scholar
[5]Rudin, W., Trigonometric series with gaps, Journ. Math. and Mech. 9 (1960), 203–228.Google Scholar
[6]Rudin, W., Fourier analysis on groups, Interscience (1962).Google Scholar