Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T13:47:31.515Z Has data issue: false hasContentIssue false
  • English
  • Français

ON BORWEIN’S CONJECTURES FOR PLANAR UNIFORM RANDOM WALKS

Part of: Quantum field theory; related classical field theories Stochastic processes

Published online by Cambridge University Press:  09 October 2019

YAJUN ZHOU Open the ORCID record for YAJUN ZHOU [Opens in a new window]
YAJUN ZHOU*
Affiliation:
Program in Applied and Computational Mathematics (PACM), Princeton University, Princeton, NJ 08544, USA Academy of Advanced Interdisciplinary Studies (AAIS), Peking University, Beijing 100871, PR China email [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 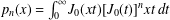$p_{n}(x)=\int _{0}^{\infty }J_{0}(xt)[J_{0}(t)]^{n}xt\,dt$ be Kluyver’s probability density for $n$-step uniform random walks in the Euclidean plane. Through connection to a similar problem in two-dimensional quantum field theory, we evaluate the third-order derivative 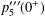$p_{5}^{\prime \prime \prime }(0^{+})$ in closed form, thereby giving a new proof for a conjecture of J. M. Borwein. By further analogies to Feynman diagrams in quantum field theory, we demonstrate that 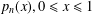$p_{n}(x),0\leq x\leq 1$ admits a uniformly convergent Maclaurin expansion for all odd integers 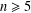$n\geq 5$, thus settling another conjecture of Borwein.

Keywords

Bessel functionsrandom walksWick rotationsTaylor expansions

MSC classification

Primary: 60G50: Sums of independent random variables; random walks 33C10: Bessel and Airy functions, cylinder functions, $_0F_1$
Secondary: 81T18: Feynman diagrams
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 107 , Issue 3 , December 2019 , pp. 392 - 411
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Footnotes

This research was supported in part by the Applied Mathematics Program within the Department of Energy (DOE) Office of Advanced Scientific Computing Research (ASCR) as part of the Collaboratory on Mathematics for Mesoscopic Modeling of Materials (CM4).

References

Bailey, D. H., Borwein, J. M., Broadhurst, D. and Glasser, M. L., ‘Elliptic integral evaluations of Bessel moments and applications’, J. Phys. A 41(20) (2008), 205203.Google Scholar
Bloch, S., Kerr, M. and Vanhove, P., ‘A Feynman integral via higher normal functions’, Compos. Math. 151(12) (2015), 2329–2375.Google Scholar
Borwein, J. M., Nuyens, D., Straub, A. and Wan, J., ‘Some arithmetic properties of random walk integrals’, Ramanujan J. 26 (2011), 109–132.Google Scholar
Borwein, J. M., Straub, A. and Vignat, C., ‘Densities of short uniform random walks in higher dimensions’, J. Math. Anal. Appl. 437(1) (2016), 668–707.Google Scholar
Borwein, J. M., Straub, A. and Wan, J., ‘Three-step and four-step random walk integrals’, Exp. Math. 22(1) (2013), 1–14.Google Scholar
Borwein, J. M., Straub, A., Wan, J. and Zudilin, W., ‘Densities of short uniform random walks’, Canad. J. Math. 64(5) (2012), 961–990. With an appendix by Don Zagier.Google Scholar
Broadhurst, D., ‘Multiple zeta values and modular forms in quantum field theory’, in: Computer Algebra in Quantum Field Theory, Texts & Monographs in Symbolic Computation (eds. Schneider, C. and Blümlein, J.) (Springer, Vienna, Austria, 2013), 33–73.Google Scholar
Broadhurst, D., ‘Feynman integrals, L-series and Kloosterman moments’, Commun. Number Theory Phys. 10(3) (2016), 527–569.Google Scholar
Broadhurst, D., ‘ L-series from Feynman diagrams with up to 22 loops’, in: Workshop on Multi-loop Calculations: Methods and Applications (Séminaires Internationaux de Recherche de Sorbonne Universités, Paris, France, 2017).Google Scholar
Broadhurst, D., ‘Combinatorics of Feynman integrals’, in: Combinatoire Algébrique, Résurgence, Moules et Applications (Centre International de Rencontres Mathématiques, Marseille-Luminy, France, 2017).Google Scholar
Broadhurst, D., ‘Feynman integrals, beyond polylogs, up to 22 loops’, in: Amplitudes 2017 (Higgs Centre for Theoretical Physics, Edinburgh, UK, 2017).Google Scholar
Broadhurst, D., ‘Combinatorics of Feynman integrals’, in: Programme on ‘Algorithmic and Enumerative Combinatorics’ (Erwin Schrödinger International Institute for Mathematics and Physics, Vienna, Austria, 2017).Google Scholar
Broadhurst, D., ‘Feynman integrals, L-series and Kloosterman moments’, in: Elliptic Integrals, Elliptic Functions and Modular Forms in Quantum Field Theory (KMPB Conference at DESY, Zeuthen, Germany, 2017).Google Scholar
Fettis, H. E., ‘On a conjecture of Karl Pearson’, in: Rider Anniversary Volume (Defense Technical Information Center, Belvoir, VA, 1963), 39–54.Google Scholar
Flajolet, P. and Sedgewick, R., Analytic Combinatorics (Cambridge University Press, Cambridge, UK, 2009).Google Scholar
Freedman, D. and Diaconis, P., ‘On the histogram as a density estimator: L 2 theory’, Z. Wahrsch. verw. Geb. 57(4) (1981), 453–476.Google Scholar
Kluyver, J. C., ‘A local probability problem’, Nederl. Acad. Wetensch. Proc. 8 (1905), 341–350.Google Scholar
Laporta, S., ‘Analytical expressions of three- and four-loop sunrise Feynman integrals and four-dimensional lattice integrals’, Internat. J. Modern Phys. A 23(31) (2008), 5007–5020.Google Scholar
Laporta, S., ‘High-precision calculation of the 4-loop contribution to the electron g - 2 in QED’, Phys. Lett. B 772(Suppl. C) (2017), 232–238.Google Scholar
Pearson, K., ‘The problem of the random walk’, Nature 72 (1905), 294.Google Scholar
Pearson, K., ‘The problem of the random walk’, Nature 72 (1905), 342.Google Scholar
Pearson, K., A Mathematical Theory of Random Migration, Drapers Company Research Memoirs: Biometric Series, III (Cambridge University Press, Cambridge, UK, 1906).Google Scholar
Lord Rayleigh, ‘The problem of the random walk’, Nature 72 (1905), 318.Google Scholar
Rogers, M., Wan, J. G. and Zucker, I. J., ‘Moments of elliptic integrals and critical L-values’, Ramanujan J. 37(1) (2015), 113–130.Google Scholar
Samart, D., ‘Feynman integrals and critical modular L-values’, Commun. Number Theory Phys. 10(1) (2016), 133–156.Google Scholar
Zhou, Y., ‘Wick rotations, Eichler integrals, and multi-loop Feynman diagrams’, Commun. Number Theory Phys. 12(1) (2018), 127–192.Google Scholar
Zhou, Y., ‘Wrońskian factorizations and Broadhurst–Mellit determinant formulae’, Commun. Number Theory Phys. 12(2) (2018), 355–407.Google Scholar
Zhou, Y., ‘Some algebraic and arithmetic properties of Feynman diagrams’, in: Elliptic Integrals, Elliptic Functions and Modular Forms in Quantum Field Theory, Texts & Monographs in Symbolic Computation (eds. Blümlein, J., Schneider, C. and Paule, P.) (Springer, Cham, Switzerland, 2019), 485–509. Ch. 19.Google Scholar
Zhou, Y., ‘On Laporta’s 4-loop sunrise formulae’, Ramanujan J. (2019), to appear. doi:10.1007/s11139-018-0090-z.Google Scholar