Hostname: page-component-f554764f5-nwwvg Total loading time: 0 Render date: 2025-04-09T08:10:16.875Z Has data issue: false hasContentIssue false
  • English
  • Français

On absolute riesz summability of Fourier series

Published online by Cambridge University Press:  09 April 2009

G. D. Dikshit
G. D. Dikshit
Affiliation:
University of Auckland, Auckland, New Zealand
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

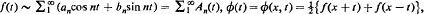Let and .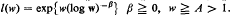

In 1951 Mohanty proved the following theorem: .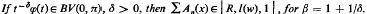

In this paper a general theorem on summability |R,l (w), 1 | of Σ An(x) has been given which improves upon Mohanty's result in different ways (see Corollaries 1, 2 and 3) and it is also shown that some of the results of this note are the best possible.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 19 , Issue 1 , February 1975 , pp. 97 - 102
Copyright
Copyright © Australian Mathematical Society 1975

References

Cheng, M. T. (1948), ‘Summability factors of Fourier series at a given point’, Duke Math. Jour. 15, 29–36.Google Scholar
Dikshit, G. D. (1958), ‘On the absolute Riesz summability factors of infinite series I’, Indian J. Math. 1, 33–40.Google Scholar
Dikshit, G. D. (1960), ‘A note on absolute Riesz summability of infinite series’, Proc. Nat. Inst. Sc. India 26A, 541–544.Google Scholar
Dikshit, G. D. (1961), ‘A summability factor theorem on the absolute Riesz summability of Fourier series’, Indian J. Math. 3, 7–26.Google Scholar
Dikshit, G. D. (1965), ‘Localization relating to the summability / R, λn, 1/ of Fourier series’, Indian J. Math. 7, 3139.Google Scholar
Dikshit, G. D. (1965), ‘On inclusion relation between Riesz and Nörlund means’, Indian J. Math. 7, 73–81.Google Scholar
Mohanty, R. (1951), ‘On the absolute Riesz summability of Fourier series and allied series’, Proc. London Math. Soc. (2) 52, 295–320.Google Scholar
Obrechkoff, N. (1928), ‘Sur la sommation absolue des séries de Dirichlet’, Comptes Rendus 186, 215–217.Google Scholar
Obrechkoff, N. (1929), ‘Über die absolute Summierung der Dirichletchen Reihen’, Math. Z. 30, 375–386.CrossRefGoogle Scholar
Tatchell, J. B. (1953), ‘On some integral transformations’, Proc. London Math. Soc. (3) 3, 257–266.CrossRefGoogle Scholar