Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-01-11T03:30:58.207Z Has data issue: false hasContentIssue false
  • English
  • Français

ON A VARIATION OF A CONGRUENCE OF SUBBARAO

Part of: Elementary number theory

Published online by Cambridge University Press:  04 February 2013

ANDREJ DUJELLA  and
FLORIAN LUCA
ANDREJ DUJELLA*
Affiliation:
Department of Mathematics, University of Zagreb, Bijenička cesta 30, 10000 Zagreb, Croatia
FLORIAN LUCA
Affiliation:
Fundación Marcos Moshinsky, Instituto de Ciencias Nucleares UNAM, Circuito Exterior, C.U., Apdo. Postal 70-543, Mexico D.F. 04510, Mexico email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study positive integers $n$ such that 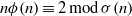$n\phi (n)\equiv 2\hspace{0.167em} {\rm mod}\hspace{0.167em} \sigma (n)$, where 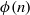$\phi (n)$ and 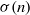$\sigma (n)$ are the Euler function and the sum of divisors function of the positive integer $n$, respectively. We give a general ineffective result showing that there are only finitely many such $n$ whose prime factors belong to a fixed finite set. When this finite set consists only of the two primes 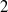$2$ and 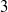$3$ we use continued fractions to find all such positive integers $n$.

Keywords

congruencesarithmetic functionscontinued fractions

MSC classification

Secondary: 11A25: Arithmetic functions; related numbers; inversion formulas 11A55: Continued fractions
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 93 , Issue 1-2 , October 2012 , pp. 85 - 90
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc.

References

Dujella, A., ‘Continued fractions and RSA with small secret exponents’, Tatra Mt. Math. Publ. 29 (2004), 101–112.Google Scholar
Dujella, A. and Jadrijević, B., ‘A family of quartic Thue inequalities’, Acta Arith. 111 (2004), 61–76.CrossRefGoogle Scholar
Guy, R., Unsolved Problems in Number Theory, 2nd edn, Problem Books in Mathematics (Springer, New York, 1994).CrossRefGoogle Scholar
He, B., Jadrijević, B. and Togbé, A., ‘Solutions of a class of quartic Thue inequalities’, Glas. Mat. Ser. III 44 (2009), 309–321.CrossRefGoogle Scholar
Hernández, S. H. and Luca, F., ‘On the largest prime factor of $(ab+ 1)(ac+ 1)(bc+ 1)$’, Bol. Soc. Mat. Mexicana 9 (2003), 235–244.Google Scholar
Lehmer, D. H., ‘On Euler’s totient function’, Bull. Amer. Math. Soc. 38 (1932), 745–751.CrossRefGoogle Scholar
Nagell, T., Introduction to Number Theory (Almqvist, Stockholm; Wiley, New York, 1951).Google Scholar
Subbarao, M. V., ‘On two congruences for primality’, Pacific J. Math. 52 (1974), 261–268.CrossRefGoogle Scholar
Worley, R. T., ‘Estimating $\vert \alpha - p/ q\vert $’, J. Aust. Math. Soc. Ser. A 31 (1981), 202–206.CrossRefGoogle Scholar