Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T14:07:37.306Z Has data issue: false hasContentIssue false
  • English
  • Français

On a theorem of Halmos concerning unbiased estimation of moments

Published online by Cambridge University Press:  09 April 2009

H. S. Konijn
H. S. Konijn
Affiliation:
Department of Economics, The City College, New York, and Cowles Foundation.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [4] Halmos considers the following situation. Let 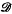be a class of distribution functions over a given (Borel) subset E of the real line, and F a function over 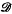. He investigates which functions F admit estimates that are unbiased over 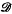and what are all possible such estimates for any given F. In particular he shows that on the basis of a sample (of size n) one can always obtain an estimate of the first moment which is unbiased in 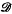and that the central moments Fm of order m ≧ 2 have estimates which are unbiased in 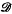if and only if n ≧ m, provided 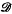satisfies the following properties: Fm exists and is finite for all distributions in 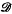and 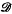includes all distributions which assign probability one to a finite number of points of E. Halmos also finds that symmetric estimates which are unbiased on 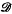are unique1 and have smaller variances on 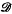than unsymmetric unbiased estimates.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 4 , Issue 2 , May 1964 , pp. 229 - 232
Copyright
Copyright © Australian Mathematical Society 1964

References

[1]Bell, C. B., Blackwell, D., and Breiman, L., On the Completeness of Order Statistics. Ann. Math. Statist. 31, (1960), 794–7.CrossRefGoogle Scholar
[2]Cramér, H.Mathematical Methods of Statistics. Princeton University Press, Princeton, (1946).Google Scholar
[3]Fraser, D. A. S., Completeness of Order Statistics. Canad. J. of Math., 6, (1954), 42–5.CrossRefGoogle Scholar
[4]Halmos, P. R., The Theory of Unbiased Estimation. Ann. Math. Statist., 17, (1946). 34–43.CrossRefGoogle Scholar
[5]Konijn, H. S., Non-Existence of Consistent Estimator Sequences and Unbiased Estimators: A Practical Example. (To appear)Google Scholar
[6]Lehmann, E. L., and Scheffé, H., Completeness, Similar Regions, and Unbiased Estimation. Sankhya, 10 (1950) 305–40; 15, (1955) 219–36.Google Scholar