Published online by Cambridge University Press: 09 April 2009
Let α be an irrational algebraic number of degree k over the rationals. Let K denote the field generated by α over the rationals and let a denote the ideal denominator of α. Then Cassels [3] has shown that for sufficiently large integral N > 0 distinctly more than half the integers n,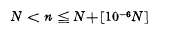 are such that (n+α)a is divisible by a prime ideal pn which does not divide (m+α)a for any integer m ≠ n satisfying
are such that (n+α)a is divisible by a prime ideal pn which does not divide (m+α)a for any integer m ≠ n satisfying 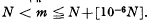 . The purpose of this note is to point out that minor modification of Cassel's proof enables the extension of the interval for n from
. The purpose of this note is to point out that minor modification of Cassel's proof enables the extension of the interval for n from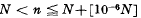 to
to 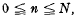 , and to derive results on the proportion of values n,
, and to derive results on the proportion of values n,  for which the values f(n) of a given integral polynomial in n are divisible by a prime p > N.
for which the values f(n) of a given integral polynomial in n are divisible by a prime p > N.