Published online by Cambridge University Press: 09 April 2009
In his paper on sets of primes with intermediate density Golomb1 proved the following theorem: Let 2 < p1 < P2 < … be any sequence of primes for which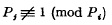 for every i and j. Denote by A (x) the number of P's not exceeding x. Then
for every i and j. Denote by A (x) the number of P's not exceeding x. Then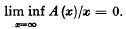 .
.
1 Golomb, S., Math. Scand. 3 (1955), 264–74.CrossRefGoogle Scholar
2 Erdös, P. and Jabotinsky, E., Indig. Math. 20 (1958), 115–128.CrossRefGoogle Scholar
3 This is Theorem 2.3 p. 230 of Prachar's book Primzahlverteilung (Springer 1957) where the literature of this question can be found.Google Scholar
4 See e.g. Erdös, P., Proc. Cambridge Phil. Soc. 34 (1957), 8.Google Scholar
5 See e.g. Landau, E., Zahlentheorie Vol. 1.Google Scholar