Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-25T04:50:22.496Z Has data issue: false hasContentIssue false
  • English
  • Français

On a many server queue with non-recurrent input and negative exponential servers

Published online by Cambridge University Press:  09 April 2009

C. Pearce
C. Pearce
Affiliation:
Department of Probability and StatisticsSheffield University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider a queueing system with k identical servers in parallel, the services being negative exponential with parameter μ. The input is a natural generalisation of the usual general recurrent input. If we denote the sequence of arrival points by {An, n ≧ 0} then the inter-arrival intervals are given by 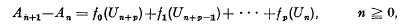where the ƒi: are (integrable) non-negative functions and {Ui} is a sequence of identically and independently distributed random variables. In the simplest case, p = 0, this is just a general recurrent input. We write U(·) for the probability distribution function of the Un.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 8 , Issue 4 , November 1968 , pp. 706 - 715
Copyright
Copyright © Australian Mathematical Society 1968

References

[1]Loynes, R. M., ‘The stability of a queue with non-independent arrival and service times’, Proc. Camb. Phil. Soc. 58 (1962), 497–520Google Scholar
[2]Kendall, D. G., ‘Stochastic processes occurring in the theory of queues and their analysis by means of the imbedded Markov chain’, Ann. Math. Statist. 24 (1953), 338–54.Google Scholar
[3]Winsten, C. B., ‘Geometric distributions in the theory of queues’, J. Roy. Statist. Soc. B 21 (1959), 1–35.Google Scholar