Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-24T14:15:40.795Z Has data issue: false hasContentIssue false
  • English
  • Français

On a lemma of L. Lorch and D. J. Newman

Published online by Cambridge University Press:  09 April 2009

Fred Ustina
Fred Ustina
Affiliation:
Department of Mathematics The University of AlbertaEdmonton 7, Canada
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [6], Lorch and Newman proved the following lemma: If g(u) is continuous and of bounded variation, 0 ≦ u ≦ 1, then (1)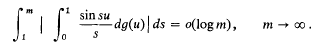. This was extended more recently by Leviatan and Lorch ([5], Lemma 3) to functions which are of bounded variation on the positive real axis, where non the upper limit of integration on the inner integral is infinite.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 15 , Issue 1 , February 1973 , pp. 78 - 85
Copyright
Copyright © Australian Mathematical Society 1973

References

[1]Bochner, S., Lectures on Fourier Integrals (Princeton University Press, Princeton (1959)).CrossRefGoogle Scholar
[2]Bochner, S. and Chandarsekharan, K., Fourier Transforms (Princeton University Press, Princeton (1949)).Google Scholar
[3]Clarkson, J. A. and Adams, C. R., ‘On definitions of bounded variation for functions of two variables’, Trans. Amer. Math. Soc. 35 (1933), 824–854.CrossRefGoogle Scholar
[4]Hobson, E. W., The Theory of Functions of a Real Variable, Vol. 11, 2ndedition. (University Press, Cambridge (1926)).Google Scholar
[5]Leviatan, D. and Lorch, L., ‘The Gibbs phenomenon and Legesgue constants for regular [J, f (x)] means’ Acta Math. Hung. 21 (1970), 65–85.CrossRefGoogle Scholar
[6]Lorch, L. and Newman, D. J., ‘The Lebesgue constants for regular Hausdorff method’, Can, Jour. Math. 13 (1961) 283–291.CrossRefGoogle Scholar
[7]McShane, E. J., Integration (Princeton University Press, Princeton (1944)).Google Scholar
[8]Young, W. H., ‘On multiple integrals’ Proc. Royal Soc. London. (A) 93 (1917), 28–41.Google Scholar
[9]Zygmund, A., Trigonometric Series, 2nd ed., Vol. II (University Press, Cambridge (1959)).Google Scholar