Let G be a finite P-group. Denote dim H1 (G, Zp) by d(G) and dimH2(G, Zp) by r(G), then d(G) is the minimal number of generators of G and G has a presentation 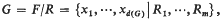where F is free on x1, …, xd(G) and R is the normal closure in F of R1, …, Rm. We have always that m ≧ r(G) = d(R/[F, R]) and we say that G belongs to a class, Gp, of the finite pgroups if m = r(G). It is well known (see for example Johnson and Wamsley (1970)) that if G and H are finite p-groups then r(G x H) = r(G) + r(H) + d(G)d(H) and hence G, H∈Gp implies Gx H∈Gp, also it is shown in Wamsley (1972) that if G is any finite pgroup then there exists an H∈Gp such that G x H belongs to Gp. Let G1 = G and Gk = Gk-1 x G then we show in this note that if G is any finite p-group, there exists an integer n(G), such that Gk∈Gp for alal k ≧ n(G).