No CrossRef data available.
Published online by Cambridge University Press: 09 April 2009
In a previous paper [1] we considered those conformally-flat Riemannian spaces which satisfy the tensorial characterisation 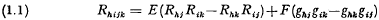 where, as usual, gij, Rhijk, Rij are the fundamental tensor, the curvature tensor, the Ricci tensor and E ≠ 0, F are certain scalars. The tensor g is always supposed to be real and analytic. A special form of the metrics of these spaces was seen to be
where, as usual, gij, Rhijk, Rij are the fundamental tensor, the curvature tensor, the Ricci tensor and E ≠ 0, F are certain scalars. The tensor g is always supposed to be real and analytic. A special form of the metrics of these spaces was seen to be 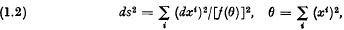 where f is any real analytic function, subject to a restriction, of the argument θ. Writing f, f′, f″,… for f(θ), df|dθ, d2f|dθ2, … the quantities E, F and the scalar curvature R of the type of spaces (1.2) were seen to be
where f is any real analytic function, subject to a restriction, of the argument θ. Writing f, f′, f″,… for f(θ), df|dθ, d2f|dθ2, … the quantities E, F and the scalar curvature R of the type of spaces (1.2) were seen to be