Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-05T15:34:36.388Z Has data issue: false hasContentIssue false
  • English
  • Français

ON 2-HOLONOMY

Part of: Fiber spaces and bundles Global differential geometry Lie algebras and Lie superalgebras

Published online by Cambridge University Press:  04 September 2019

HOSSEIN ABBASPOUR  and
FRIEDRICH WAGEMANN
HOSSEIN ABBASPOUR*
Affiliation:
Université de Nantes, 2, rue de la Houssiniere, Nantes44322, France
FRIEDRICH WAGEMANN
Affiliation:
Université de Nantes, 2, rue de la Houssiniere, Nantes44322, France e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We construct a cycle in higher Hochschild homology associated to the two-dimensional torus which represents 2-holonomy of a nonabelian gerbe in the same way as the ordinary holonomy of a principal G-bundle gives rise to a cycle in ordinary Hochschild homology. This is done using the connection 1-form of Baez–Schreiber. A crucial ingredient in our work is the possibility to arrange that in the structure crossed module 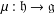$\unicode[STIX]{x1D707}:\mathfrak{h}\rightarrow \mathfrak{g}$ of the principal 2-bundle, the Lie algebra 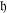$\mathfrak{h}$ is abelian, up to equivalence of crossed modules.

Keywords

a holonomy of a principal 2-bundlehigher Hochschild homologycrossed modules of Lie algebrasconnection 1-form on loop space

MSC classification

Primary: 53C08: Gerbes, differential characters
Secondary: 17B55: Homological methods in Lie (super)algebras 53C05: Connections, general theory 53C29: Issues of holonomy 55R40: Homology of classifying spaces, characteristic classes
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 110 , Issue 2 , April 2021 , pp. 145 - 174
Check for updates
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by M. Murray

References

Abbaspour, H. and Zeinalian, M., ‘String bracket and flat connections’, Algebr. Geom. Topol. 7 (2007), 197–231.CrossRefGoogle Scholar
Abbaspour, H., Tradler, T. and Zeinalian, M., ‘Algebraic string bracket as a Poisson bracket’, J. Noncommut. Geom. 4(3) (2010), 331–347.CrossRefGoogle Scholar
Baez, J. C. and Crans, A. S., ‘Higher-dimensional algebra VI: Lie 2-algebras’, Theory Appl. Categ. 12 (2004), 492–538.Google Scholar
Baez, J. C. and Schreiber, U., ‘Higher gauge theory: 2-connections on 2-bundles’, Preprint, arXiv:hep-th/0412325 (published only in abbreviated form).Google Scholar
Bartels, T., ‘2-bundles and higher gauge theory’, PhD Thesis, University of California, Riverside, CA, 2006.Google Scholar
Breen, L., ‘On the classification of 2-gerbes and 2-stacks’, Astérisque 225(9) (1994).Google Scholar
Breen, L. and Messing, W., ‘Differential geometry of gerbes’, Adv. Math. 198(2) (2005), 732–846.CrossRefGoogle Scholar
Chatterjee, S., Lahiri, A. and Sengupta, A. N., ‘Parallel transport over path spaces’, Rev. Math. Phys. 22(9) (2010), 1033–1059.CrossRefGoogle Scholar
Chen, K. T., ‘Iterated integrals of differential forms and loop space homology’, Ann. of Math. (2) 97 (1973), 217–246.CrossRefGoogle Scholar
Cuntz, J., Skandalis, G. and Tsygan, B., ‘Cyclic homology in non-commutative geometry’, in: Operator Algebras and Non-commutative Geometry, II, Encyclopaedia of Mathematical Sciences, 121 (Springer, Berlin, 2004).Google Scholar
Gawedzki, K. and Reis, N., ‘WZW branes and gerbes’, Rev. Math. Phys. 14(12) (2002), 1281–1334.CrossRefGoogle Scholar
Getzler, E., ‘Lie theory for nilpotent L ∞-algebras’, Ann. of Math. (2) 170(1) (2009), 271–301.CrossRefGoogle Scholar
Ginot, G., ‘Higher order Hochschild cohomology’, C. R. Math. Acad. Sci. Paris 346(1–2) (2008), 5–10.CrossRefGoogle Scholar
Ginot, G. and Stiénon, M., ‘G-gerbes, principal 2-group bundles and characteristic classes’, J. Symplectic Geom. 13(4) (2015), 1001–1047.CrossRefGoogle Scholar
Ginot, G., Tradler, T. and Zeinalian, M., ‘A Chen model for mapping spaces and the surface product’, Ann. Sci. Éc. Norm. Supér. (4) 43(5) (2010), 811–881.CrossRefGoogle Scholar
Giraud, J., Cohomologie Non-abélienne, Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen, 197 (Springer, Heidelberg–Tokyo–New York, 1971).CrossRefGoogle Scholar
Henriques, A., ‘Integrating L ∞ algebras’, Compos. Math. 144(4) (2008), 1017–1045.CrossRefGoogle Scholar
Laurent-Gengoux, C., Stiénon, M. and Xu, P., ‘Non-abelian differentiable gerbes’, Adv. Math. 220(5) (2009), 1357–1427.CrossRefGoogle Scholar
Loday, J.-L., ‘Spaces with finitely many non-trivial homotopy groups’, J. Pure Appl. Algebra 24 (1982), 179–202.CrossRefGoogle Scholar
Loday, J.-L., Cyclic Homology, Grundlehren der mathematischen Wissenschaften, 301 (Springer, Heidelberg–Tokyo–New York, 1992).CrossRefGoogle Scholar
Loday, J.-L., ‘Free loop space and homology’, in: Free Loop Spaces in Geometry and Topology, IRMA Lectures in Mathematics and Theoretical Physics, 24 (European Mathematical Society, Zürich, 2015), 137–156.Google Scholar
Loday, J.-L. and Kassel, C., ‘Extensions centrales d’algèbres de Lie’, Ann. Inst. Fourier (Grenoble) 32(4) (1982), 119–142.Google Scholar
Martins, J. F. and Picken, R., ‘On two-dimensional holonomy’, Trans. Amer. Math. Soc. 362(11) (2010), 5657–5695.CrossRefGoogle Scholar
Neeb, K.-H., ‘Current groups for non-compact manifolds and their central extensions’, in: Infinite Dimensional Groups and Manifolds, IRMA Lectures in Mathematics and Theoretical Physics, 5 (De Gruyter, Berlin, 2004), 109–183.Google Scholar
Neeb, K.-H., ‘Non-abelian extensions of infinite-dimensional Lie groups’, Ann. Inst. Fourier (Grenoble) 57(1) (2007), 209–271.CrossRefGoogle Scholar
Nikolaus, T. and Waldorf, K., ‘Four equivalent versions of non-abelian gerbes’, Pacific J. Math. 264(2) (2013), 355–419.CrossRefGoogle Scholar
Pirashvili, T., ‘Hodge decomposition for higher Hochschild homology’, Ann. Sci. Éc. Norm. Supér. (4) 33(2) (2000), 151–179.CrossRefGoogle Scholar
Roytenberg, D., ‘On weak Lie 2-algebras’, in: XXVI Workshop on Geometrical Methods in Physics, AIP Conference Proceedings, 956 (American Institute of Physics, Melville, NY, 2007), 180–198.Google Scholar
Sati, H., Schreiber, U. and Stasheff, J., ‘L ∞-algebra connections and applications to string and Chern–Simons n-transport’, in: Quantum Field Theory (Birkhäuser, Basel, 2009), 303–424.CrossRefGoogle Scholar
Schreiber, U. and Waldorf, K., ‘Smooth functors vs. differential forms’, Homology, Homotopy Appl. 13(1) (2011), 143–203.CrossRefGoogle Scholar
Schreiber, U. and Waldorf, K., ‘Connections on non-abelian gerbes and their holonomy’, Theory Appl. Categ. 28 (2013), 476–540.Google Scholar
Stasheff, J., ‘Differential graded Lie algebras, quasi-Hopf algebras and higher homotopy algebras’, in: Quantum Groups, Lecture Notes in Mathematics, 1510 (Springer, Berlin, 1992).Google Scholar
Tradler, T., Wilson, S. and Zeinalian, M., ‘Equivariant holonomy for bundles and abelian gerbes’, Comm. Math. Phys. 315(1) (2012), 39–108.CrossRefGoogle Scholar
Wagemann, F., ‘On Lie algebra crossed modules’, Comm. Algebra 34(5) (2006), 1699–1722.CrossRefGoogle Scholar
Wagemann, F. and Wockel, C., ‘A cocycle model for topological and Lie group cohomology’, Trans. Amer. Math. Soc. 367(3) (2015), 1871–1909.CrossRefGoogle Scholar
Wockel, C., ‘Principal 2-bundles and their gauge groups’, Forum Math. 23(3) (2011), 565–610.CrossRefGoogle Scholar