Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-02-11T12:24:16.536Z Has data issue: false hasContentIssue false
  • English
  • Français

Omitted rays and wedges of fractional Cauchy transforms

Part of: Spaces and algebras of analytic functions Miscellaneous topics of analysis in the complex domain

Published online by Cambridge University Press:  09 April 2009

R. A. Hibschweiler  and
T. H. Macgregor
R. A. Hibschweiler
Affiliation:
University of New Hampshire, Department of Mathematics and Statistics, Durham, NH 03824, USA, e-mail: [email protected]
T. H. Macgregor
Affiliation:
Bowdoin College, Department of Mathematics, Brunswick, ME 04011, USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For α > 0 let 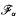α denote the set of functions which can be expressed 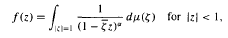where μ is a complex-valued Borel measure on the unit circle. We show that if f is an analytic function in Δ = {z ∈ 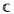: |z| < 1} and there are two nonparallel rays in 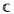/f(Δ) which do not meet, then f ∈ 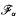α where απ denotes the largest of the two angles determined by the rays. Also if the range of a function analytic in Δ is contained in an angular wedge of opening απ and 1 < α < 2, then f ∈ 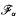α.

MSC classification

Secondary: 30E20: Integration, integrals of Cauchy type, integral representations of analytic functions 30H05: Bounded analytic functions
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 80 , Issue 3 , June 2006 , pp. 367 - 373
Copyright
Copyright © Australian Mathematical Society 2006

References

[1]Bourdon, P. and Cima, J. A. ‘On integrals of Cauchy-Stieltjes type’, Houston J. Math. 14 (1988), 465–474.Google Scholar
[2]Havin, V. P. ‘On analytic functions representable by an integral of Cauchy-Stieltijes type’, Vestnik Leningrad Univ. Ser. Mat. Meh. Astronom. 13 (1958), 66–79 (in Russian).Google Scholar
[3]Hibschweiler, R. A. and MacGregor, T. H., ‘Closure properties of families of Cauchy-Stieltjes transforms’, Proc. Amer. Math. Soc. 105 (1989), 615–621.CrossRefGoogle Scholar
[4]Hibschweiler, R. A. and MacGregor, T. H. ‘Multipliers of families of Cauchy-Stieltjes transforms’, Trans. Amer. Math. Soc. 331 (1992), 377–394.CrossRefGoogle Scholar
[5]MacGregor, T. H. ‘Analytic and univalent functions with integral representations involving complex measures’, Indiana Univ. Math. J. 36 (1987), 109–130.CrossRefGoogle Scholar
[6]MacGregor, T. H. ‘Fractional Cauchy transforms’, J. Comput. Appl. Math. 105 (1999), 93–108.CrossRefGoogle Scholar