Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-25T07:11:13.024Z Has data issue: false hasContentIssue false
  • English
  • Français

The Number of Unitarily k-Free Divisors of An Integer

Published online by Cambridge University Press:  09 April 2009

D. Suryanarayana  and
R. Sita Rama Chandra Rao
D. Suryanarayana
Affiliation:
Department of Mathematics, Andhra University Waltair, India.
R. Sita Rama Chandra Rao
Affiliation:
Department of Mathematics, Andhra University Waltair, India.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let k be a fixed integer ≧ 2. A positive integer n is called unitarily k-free, if the multiplicity of each prime factor of n is not a multiple of k; or equivalently, if n is not divisible unitarily by the k-th power of any integer > 1. By a unitary divisor, we mean as usual, a divisor d> 0 of n such that (d, n/d) = 1. The interger 1 is also considered to be unitarily k-free. The concept of a unitarily k-free integer was first introduced by Cohen (1961; §1). Let 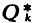denote the set of unitarily k-free integers. When k = 2, the set 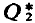coincides with the set Q* of exponentially odd integers (that is, integers in whose canonical representation each exponent is odd) discussed by Cohen himself in an earlier paper (1960; §1 and §6). A divisor d > 0 of the positive integer n is called a unitarily k-free divisor of n if d ∈ 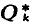. Let 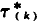(n) denote the number of unitarily k-free divisors of n.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 21 , Issue 1 , February 1976 , pp. 19 - 35
Copyright
Copyright © Australian Mathematical Society 1976

References

Cohen, E. (1960), ‘Arithmetical functions associated with the unitary divisors of an integer’, Math. Z. 74, 66–80.CrossRefGoogle Scholar
Cohen, E. (1961), ‘Some sets of integers related to the k-free integers’, Acta Sci. Math. (Szeged) 22, 223–233.Google Scholar
Hardy, G. H. and Wright, E. M. (1960), An Introduction to the Theory of Numbers (Clarendon Press, Oxford, 4th ed. 1960).Google Scholar
Kolesnik, G. A. (1969), ‘An improvement of the remainder term in the divisors problem’, Mat. Zametki 6, 545–554 = Math. Notes 6, 784–791.Google Scholar
Suryanarayana, D. and Prasad, V. Siva Rama (1973), ‘The number of k-free and k-ary divisors of m which are prime to n., J. Reine Angew Math., 264, 56–75.Google Scholar
Suryanarayana, D. and Rao, R. Sita Rama Chandra (1975), ‘Distribution of unitarily k-free integers’, J. Austral. Math. Soc. 20, 129–141.CrossRefGoogle Scholar
Suryanarayana, D. and Rao, R. Sita Rama Chandra (to appear), ‘The number of bi-unitary divisors of an integer-II’, J. Indian Math. Soc.Google Scholar