Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-01-11T04:16:41.275Z Has data issue: false hasContentIssue false
  • English
  • Français

The number of pairs of generalized integers with L.C.M. ≦ x

Published online by Cambridge University Press:  09 April 2009

D. Suryanarayana  and
V. Siva Rama Prasad
D. Suryanarayana
Affiliation:
Department of Mathematics, Andhra University, Waltair, A.P., India
V. Siva Rama Prasad
Affiliation:
Department of Mathematics, Andhra University, Waltair, A.P., India
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Generalized integers are defined in {2] as follows: Suppose there is given a finite or infinite sequence {p} of real numbers which are called generalized primes such that 1 < p1 < p2 < …. Form the set {l} of all possible p-products, i.e. the products of the form 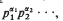where 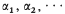are integers ≧ 0 of which all but a finite number are 0. Call these numbers generalized integers and suppose that no two generalized integers are equal if their α's are different. Then arrange {l} in an increasing sequence I = l1 < l2 < l3 < … < ln < ….

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 13 , Issue 4 , June 1972 , pp. 411 - 416
Copyright
Copyright © Australian Mathematical Society 1972

References

[1]Beurling, A., ‘Analyse de la loé asymptotique de la distribution des nombers premiers généralisés’, Acta Mathematica, 68 (1937), 255–291.CrossRefGoogle Scholar
[2]Horadam, E. M., ‘Arithmetical functions of generalized primes’, Amer. Math. Monthly, 68 (1961), 626–629.CrossRefGoogle Scholar
[3]Horadam, E. M., ‘The Euler ϕ-function for generalized integers’, Proc. Amer. Math. Soc., 14 (1963), 754–762.Google Scholar
[4]Horadam, E. M., ‘The order of Arithmetical functions of generalized integers’, Amer. Math. Monthly, 70 (1963), 506–512.Google Scholar
[5]Horadam, E. M., The number of unitary divisors of a generalized integer’, Amer. Math. Monthly, 71 (1964), 893–895.CrossRefGoogle Scholar
[6]Horadam, E. M., ‘On the number of pairs of generalized integers with least common multiple not exceeding x’, Amer. Math. Monthly, 74 (1967), 811–812.Google Scholar
[7]Suryanarayana, D., ‘The number of k-ary divisors of an integer’, Monatsh. Math., 72 (1968), 445–450.Google Scholar