Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-23T23:49:29.971Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on upper radicals in rings

Published online by Cambridge University Press:  09 April 2009

W. G. Leavitt
W. G. Leavitt
Affiliation:
University of Nebraska-Lincoln, Lincoln, Nebraska 68508, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A class (called c-radicals) is defined such that, given a c-radical P, there is in any class M′ a certain internal criterion that its upper radical UM′ = P, For P a non-c-radical (called a q-radical) there exists no smallest class M such that UM = P, and P is a q-radical if and only if for some M with P = UM there exists 0 ≠ R ∈ M such that when an image 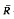¯ of R has a non-zero image in M there exists an infinite chain of epimorphisms 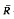¯ → R1 → R2 → … with all R1 ∈ M and no Ri, the image of any Rj, with j > i. Several examples of such rings are constructed including a ring all of whose images are primitive. Thus all radicals contained in the Jacobson radical are q-radicals.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 22 , Issue 3 , November 1976 , pp. 264 - 273
Copyright
Copyright © Australian Mathematical Society 1976

References

Divinsky, Nathan J. (1965), Rings and Radicals (Mathematical Expositions, 14, University of Toronto Press, Toronto, Ontario; Allen & Unwin, London).Google Scholar
Divinsky, Nathan J. (1975), “Unequivocal rings”, Canad. J. Math. 27, 679–690.CrossRefGoogle Scholar
Enersen, Paul O. and Leavitt, W. G. (1973), “The upper radical construction”, Publ. Math. Debrecen 20, 219–222.CrossRefGoogle Scholar
Heyman, G. A. P. and Leavitt, W. G., “A simple ring separating certain radicals”, to appear in Glasgow Math. J.Google Scholar
Sa¸siada, E. and Cohn, P. M. (1967), “An example of a simple radical ring”, J. Algebra 5, 373–377.CrossRefGoogle Scholar