Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T13:36:10.916Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON THE WEISS CONJECTURE

Part of: Graph theory Permutation groups

Published online by Cambridge University Press:  07 August 2013

NICK GILL
NICK GILL*
Affiliation:
Department of Mathematics, The Open University, Walton Hall, Milton Keynes, MK7 6AA, UK
*
[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 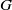$G$ be a finite group acting vertex-transitively on a graph. We show that bounding the order of a vertex stabiliser is equivalent to bounding the second singular value of a particular bipartite graph. This yields an alternative formulation of the Weiss conjecture.

Keywords

permutation groupvertex-transitivesingular valueWeiss conjecture

MSC classification

Secondary: 20B25: Finite automorphism groups of algebraic, geometric, or combinatorial structures 05C25: Graphs and abstract algebra (groups, rings, fields, etc.)
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 95 , Issue 3 , December 2013 , pp. 356 - 361
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Babai, L., Nikolov, N. and Pyber, L., ‘Product growth and mixing in finite groups’, in: Proceedings of the Nineteenth Annual ACM-SIAM Symposium on Discrete Algorithms (New York) (ACM, 2008), 248–257.Google Scholar
Bollobás, B. and Nikiforov, V., ‘Hermitian matrices and graphs: singular values and discrepancy’, Discrete Math. 285 (1–3) (2004), 17–32.CrossRefGoogle Scholar
Gill, N., ‘Quasirandom group action’, J. Eur. Math. Soc. (JEMS), to appear. arXiv:1302.1186.Google Scholar
Gowers, W. T., ‘Quasirandom groups’, Combin. Probab. Comput. 17 (2008), 363–387.CrossRefGoogle Scholar
Lubotzky, A., ‘Discrete groups, expanding graphs and invariant measures’, in: Modern Birkhäuser Classics (Birkhäuser, Basel, 2010), with an appendix by Jonathan D. Rogawski, reprint of the 1994 edition.Google Scholar
Potočnik, P., Spiga, P. and Verret, G., ‘On graph-restrictive permutation groups’, J. Combin. Theory Ser. B 102 (3) (2012), 820–831.CrossRefGoogle Scholar
Praeger, C., Pyber, L., Spiga, P. and Szabó, E., ‘Graphs with automorphism groups admitting composition factors of bounded rank’, Proc. Amer. Math. Soc. 140 (7) (2012), 2307–2318.CrossRefGoogle Scholar
Sabidussi, G., ‘Vertex-transitive graphs’, Monatsh. Math. 68 (1964), 426–438.CrossRefGoogle Scholar
Weiss, R., ‘s-transitive graphs’, in: Algebraic Methods in Graph Theory, Vol. I, II (Szeged, 1978), Vol. 25, Colloq. Math. Soc. János Bolyai (North-Holland, Amsterdam, 1981), 827–847.Google Scholar