Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-25T10:56:33.418Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON THE INTERSECTIONS OF THE BESICOVITCH SETS AND ERDŐS–RÉNYI SETS

Part of: Probabilistic theory: distribution modulo $1$; metric theory of algorithms Classical measure theory

Published online by Cambridge University Press:  01 February 2019

JINJUN LI  and
MIN WU
JINJUN LI
Affiliation:
School of Mathematics and Information Science, Guangzhou University, Guangzhou 510006, PR China email [email protected]
MIN WU*
Affiliation:
Department of Mathematics, South China University of Technology, Guangzhou 510641, PR China email [email protected]
*
✉[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For 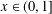$x\in (0,1]$ and a positive integer 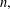$n,$ let 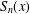$S_{\!n}(x)$ denote the summation of the first $n$ digits in the dyadic expansion of $x$ and let 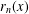$r_{n}(x)$ denote the run-length function. In this paper, we obtain the Hausdorff dimensions of the following sets:

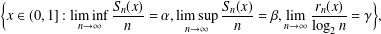$$\begin{eqnarray}\bigg\{x\in (0,1]:\liminf _{n\rightarrow \infty }\frac{S_{\!n}(x)}{n}=\unicode[STIX]{x1D6FC},\limsup _{n\rightarrow \infty }\frac{S_{\!n}(x)}{n}=\unicode[STIX]{x1D6FD},\lim _{n\rightarrow \infty }\frac{r_{n}(x)}{\log _{2}n}=\unicode[STIX]{x1D6FE}\bigg\},\end{eqnarray}$$
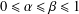where $0\leq \unicode[STIX]{x1D6FC}\leq \unicode[STIX]{x1D6FD}\leq 1$, 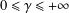$0\leq \unicode[STIX]{x1D6FE}\leq +\infty$.

Keywords

Besicovitch setsErdős–Rényi setsHausdorff dimension

MSC classification

Primary: 28A80: Fractals 11K55: Metric theory of other algorithms and expansions; measure and Hausdorff dimension
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 108 , Issue 1 , February 2020 , pp. 33 - 45
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author was supported by the National Natural Science Foundation of China (11671189) and the Natural Science Foundation of Fujian Province (2017J01403). The second author was supported by the National Natural Science Foundation of China (11771153).

References

Barreira, L., Saussol, B. and Schmeling, J., ‘Distribution of sequences of digits via multifractal analysis’, J. Number Theory 97 (2002), 410–438.Google Scholar
Besicovitch, A., ‘On the sum of digits of real numbers represented in the dyadic system’, Math. Ann. 110 (1934), 321–330.Google Scholar
Carbone, L., Cardone, G. and Esposito, A. C., ‘Binary digits expansion of numbers: Hausdorff dimensions of intersections of level sets of averages’ upper and lower limits’, Sci. Math. Jpn. 60 (2004), 347–356.Google Scholar
Chen, H. B. and Wen, Z. X., ‘The fractional dimensions of intersections of the Besicovitch sets and the Erdős–Rényi sets’, J. Math. Anal. Appl. 401 (2013), 29–37.Google Scholar
Chen, H. B. and Yu, M., ‘A generalization of the Erdős–Rényi limit theorem and the corresponding multifractal analysis’, J. Number Theory 192 (2018), 307–327.Google Scholar
Eggleston, H. G., ‘The fractional dimension of a set defined by decimal properties’, Q. J. Math. 20 (1949), 31–36.Google Scholar
Erdős, P. and Rényi, A., ‘On a new law of large numbers’, J. Anal. Math. 22 (1970), 103–111.Google Scholar
Falconer, K. J., Fractal Geometry: Mathematical Foundations and Applications (John Wiley, Chichester, 1990), Chapter 2, 27–36; Chapter 8, 110–113.Google Scholar
Fan, A. H., Liao, L., Ma, J. and Wang, B., ‘Dimension of Besicovitch–Eggleston sets in countable symbolic space’, Nonlinearity 23 (2010), 1185–1197.Google Scholar
Fang, L. L., Song, S. K. and Wu, M., ‘Exceptional sets related to the run-length function of beta-expansions’, Fractals 26 (2018), 1850049.Google Scholar
Feng, D. J., Wen, Z. Y. and Wu, J., ‘Some dimensional results for homogeneous Moran sets’, Sci. China Ser. A 40 (1997), 172–178.Google Scholar
Hawkes, J., ‘Some algebraic properties of small sets’, Q. J. Math. 26 (1975), 195–201.Google Scholar
Li, J. J. and Li, B., ‘Hausdorff dimensions of some irregular sets associated with 𝛽-expansions’, Sci. China Math. 3(59) (2016), 445–458.Google Scholar
Li, J. J. and Wu, M., ‘On exceptional sets in Erdős–Rényi limit theorem’, J. Math. Anal. Appl. 436 (2016), 355–365.Google Scholar
Li, J. J. and Wu, M., ‘On exceptional sets in Erdős–Rényi limit theorem revisited’, Monatsh. Math. 182 (2017), 865–875.Google Scholar
Li, J. J. and Wu, M., ‘On the intersections of the Besicovitch sets and exceptional sets in Erdős–Rényi limit theorem’, Acta Math. Hungar., to appear. Published online (3 January 2019).Google Scholar
Li, J. J., Wu, M. and Xiong, Y., ‘Hausdorff dimensions of the divergence points of self-similar measures with the open set condition’, Nonlinearity 25 (2012), 93–105.Google Scholar
Li, J. J., Wu, M. and Yang, X. F., ‘On the longest block in Lüroth expansion’, J. Math. Anal. Appl. 457 (2018), 522–532.Google Scholar
Li, W. X. and Dekking, F. M., ‘Hausdorff dimensions of subsets of Moran fractals with prescribed group frequency of their codings’, Nonlinearity 16 (2003), 1–13.Google Scholar
Ma, J. H., Wen, S. Y. and Wen, Z. Y., ‘Egoroff’s theorem and maximal run length’, Monatsh. Math. 151 (2007), 287–292.Google Scholar
Olsen, L., ‘Distribution of digits in integers: Besicovitch–Eggleston subsets of ℕ’, J. Lond. Math. Soc. 67 (2003), 561–579.Google Scholar
Olsen, L., ‘A generalization of a result by W. Li and F. Dekking on the Hausdorff dimensions of subsets of self-similar sets with prescribed group frequency of their codings’, Aequationes Math. 72 (2006), 10–26.Google Scholar
Révész, P., Random Walk in Random and Non-Random Environments, 2nd edn (World Scientific, Singapore, 2005), 59–61.Google Scholar
Sun, Y. and Xu, J., ‘A remark on exceptional sets in Erdős–Rényi limit theorem’, Monatsh. Math. 184 (2017), 291–296.Google Scholar
Tong, X., Yu, Y. L. and Zhao, Y. F., ‘On the maximal length of consecutive zero digits of 𝛽-expansion’, Int. J. Number Theory 12 (2016), 625–633.Google Scholar
Zhang, M. J. and Peng, L., ‘On the interesctions of the Besicovitch sets and the Erdős–Rényi sets’, Monatsh. Math. , to appear. Published online (23 June 2018).Google Scholar
Zou, R. B., ‘Hausdorff dimension of the maximal run-length in dyadic expansion’, Czechoslovak Math. J. 61 (2011), 881–888.Google Scholar