Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-24T22:33:31.529Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on the idempotent measures on countable semigroups

Published online by Cambridge University Press:  09 April 2009

Tze-Chien Sun  and
N. A. Tserpes
Tze-Chien Sun
Affiliation:
Wayne State University and University of South Florida
N. A. Tserpes
Affiliation:
Wayne State University and University of South Florida
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [6] we announced the followingConjecture: Let S be a locally compact semigroup and let μ be an idempotent regular probability measure on S with support F. Then

(a) F is a closed completely simple subsemigroup.

(b) F is isomorphic both algebraically and topologically to a paragroup ([2], p.46) X × G × Y where X and Y are locally compact left-zero and right-zero semi-groups respectively and G is a compact group. In X × G × Y the topology is the product topology and the multiplication of any two elements is defined by 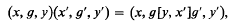, x where [y, x′] is continuous mapping from Y × X → G.

(c) The induced μ on X × G × Y can be decomposed as a product measure μX × μG× μY where μX and μY are two regular probability measures on X and Y respectively and μG is the normed Haar measure on G.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 11 , Issue 4 , November 1970 , pp. 417 - 420
Copyright
Copyright © Australian Mathematical Society 1970

References

[1]Clifford, A. H. and Preston, G. B., The algebraic theory of semigroups, Vol. 1, (Mathematical Surveys, No. 7, American Math. Society, 1961).Google Scholar
[2]Berglund, J. F. and Hofmann, K. H., Compact semitopological semigroups and weakly periodic functions (Springer Lecture Notes No. 42, 1967).CrossRefGoogle Scholar
[3]Heble, M. and Rosenblatt, M., ‘Idempotent measures on a compact topological semigroup’, Proc. Amer. Math. Soc. 14 (1963), 177–184.CrossRefGoogle Scholar
[4]Martin-Lof, P., ‘Probability theory on discrete semigroups’, Z. Wahrscheinlichkeitstheorie verw. Geb. 4 (1966), 78–102.CrossRefGoogle Scholar
[5]Pym, J. S., ‘Idempotent measures on semigroups’, Pacific J. of Math. 12 (1962), 685–698.CrossRefGoogle Scholar
[6]Sun, Tze-Chien and Tserpes, N. A., ‘Idempotent measures on locally compact semigroups’, Z. Wahrscheinlichkeitstheorie verw. Geb. (to appear).Google Scholar
[7]Tortrat, A., ‘Lois tendues sur un demi-groupe topologique complètement simple’, Z. Wahrscheinlichkeitstheorie verw. Geb. 6 (1966), 145–160.CrossRefGoogle Scholar
[8]Tserpes, N. A. and Sun, Tze-Chien, ‘Idempotent probability measures on locally compact abelian semigroups’, Jour. Math. Mech. (to appear, 07, 1970).Google Scholar