Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T18:37:13.005Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON THE FREIMAN AND BALOG–SZEMERÉDI–GOWERS THEOREMS IN FINITE FIELDS

Part of: Sequences and sets

Published online by Cambridge University Press:  01 February 2009

BEN GREEN  and
TERENCE TAO
BEN GREEN*
Affiliation:
Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK (email: [email protected])
TERENCE TAO
Affiliation:
Department of Mathematics, UCLA, Los Angeles CA 90095-1555, USA (email: [email protected])
*
✉For correspondence; e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove quantitative versions of the Balog–Szemerédi–Gowers and Freiman theorems in the model case of a finite field geometry 𝔽2n, improving the previously known bounds in such theorems. For instance, if 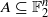is such that ∣A+A∣≤K∣A∣ (thus A has small additive doubling), we show that there exists an affine subspace H of 𝔽2n of cardinality 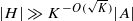such that 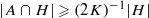. Under the assumption that A contains at least ∣A∣3/K quadruples with a1+a2+a3+a4=0, we obtain a similar result, albeit with the slightly weaker condition ∣H∣≫K−O(K)∣A∣.

Keywords

Freiman’s theoremfinite field modelsBalog–Szemerédi–Gowers theorem

MSC classification

Secondary: 11B99: None of the above, but in this section
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 86 , Issue 1 , February 2009 , pp. 61 - 74
Copyright
Copyright © Australian Mathematical Society 2009

Footnotes

The first author is a Clay Research Fellow, and is pleased to acknowledge the support of the Clay Mathematics Institute. The second author is supported by a grant from the MacArthur Foundation.

References

[1]Balog, A. and Szemerédi, E., ‘A statistical theorem of set addition’, Combinatorica 14 (1994), 263–268.CrossRefGoogle Scholar
[2]Gowers, W. T., ‘A new proof of Szemerédi’s theorem for arithmetic progressions of length four’, Geom. Funct. Anal. 8 (1998), 529–551.Google Scholar
[3]Gowers, W. T., ‘A new proof of Szemerédi’s theorem’, Geom. Funct. Anal. 11(3) (2001), 465–588.CrossRefGoogle Scholar
[4]Green, B. J., ‘The polynomial Freiman–Ruzsa conjecture’, unpublished notes. Available at http://www.dpmms.cam.ac.uk/∼bjg23.Google Scholar
[5]Green, B. J. and Sanders, T., ‘Boolean functions with small spectral norm’, Geom. Funct. Anal. 18(1) (2008), 144–162.CrossRefGoogle Scholar
[6]Green, B. J. and Tao, T. C., ‘An inverse theorem for the Gowers U 3-norm, with applications’, Proc. Edinb. Math. Soc. 51(1) (2008), 73–153.CrossRefGoogle Scholar
[7]Green, B. J. and Tao, T. C., ‘Freiman’s theorem in finite fields via extremal set theory’, Preprint.Google Scholar
[8]Ruzsa, I. Z., ‘An analog of Freiman’s theorem in groups. Structure theory of set addition’, Astérisque 258 (1999), 323–326.Google Scholar
[9]Sanders, T., ‘A note on Freiman’s theorem in vector spaces’, Combin. Probab. Comput. 17(2) (2008), 297–305.CrossRefGoogle Scholar
[10]Tao, T. C. and Vu, V. H., Additive Combinatorics (Cambridge University Press, Cambridge, 2006).CrossRefGoogle Scholar