Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-28T14:24:30.001Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on right invariant integrals on locally compact semigroups

Published online by Cambridge University Press:  09 April 2009

U. B. Tewari
U. B. Tewari
Affiliation:
Department of MathematicsPanjab UniversityChandigarh, India
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An integral on a locally compact Hausdorff semigroup S is a nontrivial, positive linear function μ on the space K(S) of real-valued continuous functions on S with compact support. If S has the property: 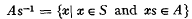is compact whenever A is compact subset of S and s ∈ S, then the function fa defined by fa(x) = f(xa) is in K(S) whenever f ∈ K(S) and a ∈ S An integral on a locally compact semigroup S with the property (P) is said to be right invariant if μ(fa) = μ(f) for all f ∈ K(S) and a ∈ S.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 8 , Issue 3 , August 1968 , pp. 512 - 514
Copyright
Copyright © Australian Mathematical Society 1968

References

[1]Michael, J. H., ‘Right invariant integrals on locally compact semigroup’, J. Aust. Math. Soc. 4 (1964), 273–286.Google Scholar
[2]Nachbin, L., The Haar Integral (Van Nostrand Company, New York, 1965).Google Scholar
[3]Rosen, W. G., ‘On the invariant means over compact semigroups’, Proc. Amer. Math. Soc. 7 (1956), 1076–1082.CrossRefGoogle Scholar
[4]Granirer, E., ‘On amenable semigroups with a finite dimensional set of invariant means I’, Illinois J. of Math. 7 (1963), 32–48.Google Scholar
[5]Granirer, E., ‘On amenable semigroups with a finite dimensional set of invariant means II’, Illinois J. of Math. 7 (1963) 49–58.Google Scholar