Published online by Cambridge University Press: 09 April 2009
Consider a positive regular Markov chain X0, X1, X2,… with s(s finite) number of states E1, E2,… E8, and a transition probability matrix P = (pij) where = 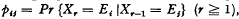 , and an initial probability distribution given by the vector p0. Let {Zr} be a sequence of random variables such that
, and an initial probability distribution given by the vector p0. Let {Zr} be a sequence of random variables such that 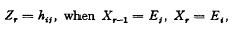 and consider the sum SN = Z1+Z2+ … ZN. It can easily be shown that (cf. Bartlett [1] p. 37),
and consider the sum SN = Z1+Z2+ … ZN. It can easily be shown that (cf. Bartlett [1] p. 37), 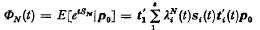 where λ1(t), λ2(t)…λ1(t) are the latent roots of P(t) ≡ (pijethij) and si(t) and t′i(t) are the column and row vectors corresponding to λi(t), and so constructed as to give t′i(t)Si(t) = 1 and t′i(t), si(o) = si where t′i(t) and si are the corresponding column and row vectors, considering the matrix
where λ1(t), λ2(t)…λ1(t) are the latent roots of P(t) ≡ (pijethij) and si(t) and t′i(t) are the column and row vectors corresponding to λi(t), and so constructed as to give t′i(t)Si(t) = 1 and t′i(t), si(o) = si where t′i(t) and si are the corresponding column and row vectors, considering the matrix 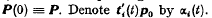 .
.