Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-26T20:27:59.313Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on centre-by-finite-exponent varieties of groups

Published online by Cambridge University Press:  09 April 2009

Narain Gupta  and
Akbar Rhemtulla
Narain Gupta
Affiliation:
University of Manitoba
Akbar Rhemtulla
Affiliation:
University of Alberta, Edmonton
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We refer the reader to Hanna Neumann [7] for notation and other undefined terms. Let 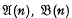and 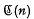denote the varieties of groups defined by the laws (xy)n=xnyn, [x, y]n=1 and [x, yn]respectively, where n is an integer. 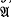(n)-groups were termed “n-abelian” by R. Baer [1] and have been a subject matter of investigation by various authors (see [3], [5], [6] and the references therein). Recently KaluŽnin [5] has shown that 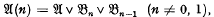, thus clarifying the relationship between U(n) and the familiar varieties. From the elementary inequalities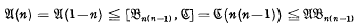(n ≠ 0,1)it is easily deduced that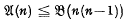(see for instance [5]). 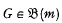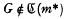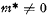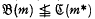If G = Cm Wr C∞, then cleary but for any Thus and 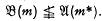. It is also easy to see that in general 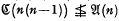(see for instance [6] § 5.1) and we are led to ask

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 11 , Issue 1 , February 1970 , pp. 33 - 36
Copyright
Copyright © Australian Mathematical Society 1970

References

[1]Baer, R., ‘Factorization of n-soluble and n-nilpotent groups’, Proc. Amer. Math. Soc. 4 (1953), 15–26.Google Scholar
[2]Dlab, V., ‘A note on powers of a group’, Acta. Sci. Math. (Szeged) 25 (1964), 177–178.Google Scholar
[3]Durbin, J. R., ‘Commutativity and n-abelian groups’, Math. Zeitschr. 98 (1967), 89–92.CrossRefGoogle Scholar
[4]Hardy, G. H. and Wright, E. M., Theory of Numbers, (Oxford 1965).Google Scholar
[5]KaluŽnin, L. A., ‘The structure of n-abelian groups’ (Russian), Mat. Zametki 2 (1967), 455–462.Google Scholar
[6]Karasev, G. A., ‘The concept of n-nilpotent groups’, Sibirskii Mat. Zhurnal 7 (1966), 1014–1032. English Translation pp. 808–821.Google Scholar
[7]Neumann, Hanna, Varieties of Groups, (Springer-Verlag). 1967.CrossRefGoogle Scholar
[8]Schur, I., ‘Über die Darstellung der endlichen Gruppen durch gebrochene lineare subsitutionen’, J. reine angew. Math. 27 (1904), 20–50.Google Scholar