Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T23:29:16.826Z Has data issue: false hasContentIssue false
  • English
  • Français

Normal surfaces in non-compact 3-manifolds

Part of: Low-dimensional topology

Published online by Cambridge University Press:  09 April 2009

Ensil Kang
Ensil Kang
Affiliation:
Department of MathematicsCollege of Natural Sciences Chosun UniversityGwangju 501-759Korea e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We extend the normal surface Q-theory to non-compact 3-manifolds with respect to ideal triangulations. An ideal triangulation of a 3-manifold often has a small number of tetrahedra resulting in a system of Q-matching equations with a small number of variables. A unique feature of our approach is that a compact surface F with boundary properly embedded in a non-compact 3-manifold M with an ideal triangulation with torus cusps can be represented by a normal surface in M as follows. A half-open annulus made up of an infinite number of triangular disks is attached to each boundary component of F. The resulting surface 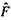, when normalized, will contain only a finite number of Q-disks and thus correspond to an admissible solution to the system of Q-matching equations. The correspondence is bijective.

Keywords

3-manifoldnormal surfaceknot

MSC classification

Secondary: 57M99: None of the above, but in this section 57M10: Covering spaces
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 78 , Issue 3 , June 2005 , pp. 305 - 321
Copyright
Copyright © Australian Mathematical Society 2005

References

[1]Burton, B., Jaco, W., Letscher, D. and Rubinstein, J. H., ‘Algorithms to find connected sum and torus decompositions of 3-manifolds’, preprint, 2000.Google Scholar
[2]Burton, B. and Rubinstein, J. H., in preparation.Google Scholar
[3]Haken, W., ‘Theorie der Normalflächen’, Acta Math. 105 (1961), 245–375.CrossRefGoogle Scholar
[4]Jaco, W., ‘Personal notes’, unpublished, 1987.Google Scholar
[5]Jaco, W. and Oertel, U., ‘An algorithm to decide if a 3-manifold is a Haken manifold’, Topology 23 (1984), 195–209.CrossRefGoogle Scholar
[6]Jaco, W. and Rubinstein, J. H., ‘PL equivariant surgery and invariant decompositions of 3-manifolds’, Advances in Math. 73 (1989), 149–191.CrossRefGoogle Scholar
[7]Jaco, W. and Tollefson, J. L., ‘Algorithms for the complete decomposition of a closed 3-manifold’, Illionis J. Math. 39 (1995), 358–406.Google Scholar
[8]Kang, E., ‘Normal surfaces in the figure-8 knot complement’, J. Knot Theory Ramificantions 12 (2004), 269–279.CrossRefGoogle Scholar
[9]Kang, E., Normal surfaces in knot compements (Ph.D. Thesis, University of Connecticut, 1999).Google Scholar
[10]Thompson, A., ‘Thin position and the recognition problem for S3’, Math. Res. Lett. 1 (1994), 613–630.CrossRefGoogle Scholar
[11]Tollefson, J. L., ‘Normal surface Q-theory’, Pacific J. Math. 183 (1998), 359–374.CrossRefGoogle Scholar
[12]Weeks, J. R., ‘Snappea: A computer program for creating and studying hyperbolic 3-manifolds’, available by anonymous ftp from geom. umn. edu/pub/softwarw/snappea.Google Scholar