Let 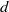$d$ and $n$ be positive integers such that 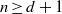$n\geq d+ 1$ and 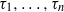${\tau }_{1} , \ldots , {\tau }_{n} $ integers such that 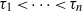${\tau }_{1} \lt \cdots \lt {\tau }_{n} $. Let 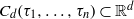${C}_{d} ({\tau }_{1} , \ldots , {\tau }_{n} )\subset { \mathbb{R} }^{d} $ denote the cyclic polytope of dimension 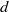$d$ with $n$ vertices 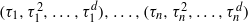$({\tau }_{1} , { \tau }_{1}^{2} , \ldots , { \tau }_{1}^{d} ), \ldots , ({\tau }_{n} , { \tau }_{n}^{2} , \ldots , { \tau }_{n}^{d} )$. We are interested in finding the smallest integer 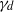${\gamma }_{d} $ such that if 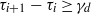${\tau }_{i+ 1} - {\tau }_{i} \geq {\gamma }_{d} $ for 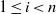$1\leq i\lt n$, then 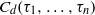${C}_{d} ({\tau }_{1} , \ldots , {\tau }_{n} )$ is normal. One of the known results is 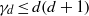${\gamma }_{d} \leq d(d+ 1)$. In the present paper a new inequality 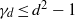${\gamma }_{d} \leq {d}^{2} - 1$ is proved. Moreover, it is shown that if 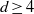$d\geq 4$ with 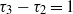${\tau }_{3} - {\tau }_{2} = 1$, then 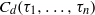${C}_{d} ({\tau }_{1} , \ldots , {\tau }_{n} )$ is not very ample.