Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-09T08:33:50.923Z Has data issue: false hasContentIssue false
  • English
  • Français

NON-NEHARI-MANIFOLD METHOD FOR ASYMPTOTICALLY LINEAR SCHRÖDINGER EQUATION

Part of: Elliptic equations and systems

Published online by Cambridge University Press:  10 October 2014

X. H. TANG
X. H. TANG*
Affiliation:
School of Mathematics and Statistics, Central South University, Changsha, Hunan 410083, PR China email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider the semilinear Schrödinger equation

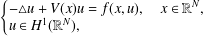$$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}-\triangle u+V(x)u=f(x,u),\quad x\in \mathbb{R}^{N},\\ u\in H^{1}(\mathbb{R}^{N}),\end{array}\right.\end{eqnarray}$$
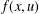where $f(x,u)$ is asymptotically linear with respect to $u$, 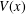$V(x)$ is 1-periodic in each of 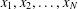$x_{1},x_{2},\dots ,x_{N}$ and 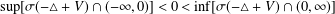$\sup [{\it\sigma}(-\triangle +V)\cap (-\infty ,0)]<0<\inf [{\it\sigma}(-\triangle +V)\cap (0,\infty )]$. We develop a direct approach to find ground state solutions of Nehari–Pankov type for the above problem. The main idea is to find a minimizing Cerami sequence for the energy functional outside the Nehari–Pankov manifold 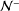${\mathcal{N}}^{-}$ by using the diagonal method.

Keywords

Schrödinger equationasymptotically linearnon-Nehari-manifold methodground state solutions of Nehari–Pankov type

MSC classification

Primary: 35J20: Variational methods for second-order elliptic equations
Secondary: 35J60: Nonlinear elliptic equations
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 98 , Issue 1 , February 2015 , pp. 104 - 116
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Ding, Y., Variational Methods for Strongly Indefinite Problems (World Scientific, Singapore, 2007).Google Scholar
Ding, Y. and Lee, C., ‘Multiple solutions of Schrödinger equations with indefinite linear part and super or asymptotically linear terms’, J. Differential Equations 222 (2006), 137–163.CrossRefGoogle Scholar
Edmunds, D. E. and Evans, W. D., Spectral Theory and Differential Operators (Clarendon Press, Oxford, 1987).Google Scholar
Egorov, Y. and Kondratiev, V., On Spectral Theory of Elliptic Operators (Birkhäuser, Basel, 1996).Google Scholar
Jeanjean, J., ‘On the existence of bounded Palais–Smale sequence and application to a Landesman–Lazer-type problem on ℝN’, Proc. Roy. Soc. Edinburgh Sect. A 129 (1999), 787–809.Google Scholar
Kryszewski, W. and Szulkin, A., ‘Generalized linking theorem with an application to a semilinear Schrödinger equation’, Adv. Differential Equations 3 (1998), 441–472.Google Scholar
Li, G. B. and Szulkin, A., ‘An asymptotically periodic Schrödinger equation with indefinite linear part’, Commun. Contemp. Math. 4 (2002), 763–776.Google Scholar
Lions, P. L., ‘The concentration–compactness principle in the calculus of variations. The locally compact case, part 2’, Ann. Inst. H. Poincaré Anal. Non Linéaire 1 (1984), 223–283.Google Scholar
Pankov, A., ‘Periodic nonlinear Schrödinger equation with application to photonic crystals’, Milan J. Math. 73 (2005), 259–287.CrossRefGoogle Scholar
Szulkin, A. and Weth, T., ‘Ground state solutions for some indefinite variational problems’, J. Funct. Anal. 257 (2009), 3802–3822.CrossRefGoogle Scholar
Szulkin, A. and Zou, W. M., ‘Homoclinic orbits for asymptotically linear Hamiltonian systems’, J. Funct. Anal. 187 (2001), 25–41.Google Scholar
Tang, X. H., ‘New conditions on nonlinearity for a periodic Schrödinger equation having zero as spectrum’, J. Math. Anal. Appl. 413 (2014), 392–410.Google Scholar
Tang, X. H., ‘New super-quadratic conditions on ground state solutions for superlinear Schrödinger equation’, Adv. Nonlinear Stud. 14 (2014), 361–374.Google Scholar
Tang, X. H., ‘Non-Nehari manifold method for superlinear Schrödinger equation’, Taiwanese J. Math. 18 (2014), 1950–1972.Google Scholar
Tang, X. H., Ground state solutions of Nehari–Pankov type for asymptotically periodic Schrödinger equation, Preprint, arXiv:1405.2607v1 [math.AP], 12 May 2014.Google Scholar
Willem, M., Minimax Theorems (Birkhäuser, Boston, MA, 1996).CrossRefGoogle Scholar