Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-24T12:31:50.244Z Has data issue: false hasContentIssue false
  • English
  • Français

A non-existence theorem for (v, k,λ)-graphs

Published online by Cambridge University Press:  09 April 2009

W. D. Wallis
W. D. Wallis
Affiliation:
Department of MathematicsLa Trobe UniversityBundoora, Victoria 3083
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A (ν, κ, λ)-graph is defined in [3] as a graph on ν points, each of valency κ, and such that for any two points P and Q there are exactly λ points which are joined to both. In other words, if Si is the set of points joined to Pi, then

Si has k elements for any i

Si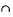Sj has λ elements if i≠j

The sets Si are the blocks of a (v, k, λ)-configuration, so a necessary condition on v, k, and λ that a graph should exist is that a (v, k, λ)- configuration should exist. Another necessary condition, reported by Bose (see [1]) and others, is that there should be an integer m satisfying 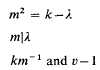have equal parity. We shall prove that these conditions are not sufficient.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 11 , Issue 3 , August 1970 , pp. 381 - 383
Copyright
Copyright © Australian Mathematical Society 1970

References

[1]Ahrens, R. W. and Szekeres, C., ‘On a combinatorial generalization of twenty-seven lines associated with a cubic surface’, J. Australian Math. Soc. 10 (1969), 465–492.CrossRefGoogle Scholar
[2]Hall, Marshall Jr, Combinatorial Theory (Blaisdell, 1967).Google Scholar
[3]Wallis, W. D., ‘Certain graphs arising from Hadamard matrices’, Bull. Australian Math. Soc. 1 (1969), 325–331.CrossRefGoogle Scholar