Hostname: page-component-848d4c4894-r5zm4 Total loading time: 0 Render date: 2024-07-03T04:23:57.301Z Has data issue: false hasContentIssue false
  • English
  • Français

A non-cyclic one-relator group all of whose finite quotients are cyclic

To Bernhard Hermann Neumann on his 60th birthday

Published online by Cambridge University Press:  09 April 2009

Gilbert Baumslag
Gilbert Baumslag
Affiliation:
Institute for Advanced Study and Rice University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

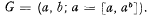Let G be a group on two generators a and b subject to the single defining relation a = [a, ab]: . As usual [x, y] = x−1y−1xy and xy = y−1xy if x and y are elements of a group. The object of this note is to show that every finite quotient of G is cyclic. This implies that every normal subgroup of G contains the derived group G′. But by Magnus' theory of groups with a single defining relation G′ ≠ 1 ([1], §4.4). So G is not residually finite. This underlines the fact that groups with a single defining relation need not be residually finite (cf. [2]).

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 10 , Issue 3-4 , November 1969 , pp. 497 - 498
Copyright
Copyright © Australian Mathematical Society 1969

References

[1]Magnus, W., Karrass, A. and Solitar, D., Combinatorial Group Theory (Interscience Publishers, 1966).Google Scholar
[2]Baumslag, G. and Solitar, D., ‘Some two-generator one-relator nonhopfian groups’, Bull. Amer. Math. Soc. 68 (1962), 199–201.CrossRefGoogle Scholar
[3]Higman, G., ‘A finitely generated infinite simple group’, J. London Math. Soc. 26 (1951), 61–64.CrossRefGoogle Scholar