No CrossRef data available.
Article contents
A NILPOTENCY-LIKE CONDITION FOR INFINITE GROUPS
Published online by Cambridge University Press: 28 March 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
If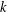 
$k$ is a positive integer, a group 
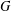$G$ is said to have the 
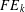$FE_{k}$-property if for each element 
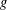$g$ of 
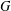$G$ there exists a normal subgroup of finite index 
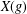$X(g)$ such that the subgroup 
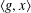$\langle g,x\rangle$ is nilpotent of class at most 
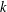$k$ for all 
$x\in X(g)$. Thus,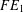 
$FE_{1}$-groups are precisely those groups with finite conjugacy classes (
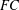$FC$-groups) and the aim of this paper is to extend properties of 
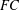$FC$-groups to the case of groups with the 
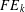$FE_{k}$-property for 
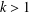$k>1$. The class of 
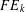$FE_{k}$-groups contains the relevant subclass 
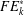$FE_{k}^{\ast }$, consisting of all groups 
$G$ for which to every element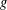 
$g$ there corresponds a normal subgroup of finite index 
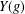$Y(g)$ such that 
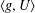$\langle g,U\rangle$ is nilpotent of class at most 
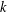$k$, whenever 
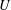$U$ is a nilpotent subgroup of class at most 
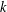$k$ of 
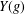$Y(g)$.
Keywords
MSC classification
Secondary:
20F45: Engel conditions
- Type
- Research Article
- Information
- Copyright
- © 2018 Australian Mathematical Publishing Association Inc.
References
Ballester Bolinches, A. and Pedraza Aguilera, M. C., ‘On finite soluble products of N-connected groups’, J. Group Theory
2 (1999), 291–299.Google Scholar
Bastos, R. and Shumyatsky, P., ‘On profinite groups with Engel-like conditions’, J. Algebra
427 (2015), 215–225.Google Scholar
Beidleman, J. C. and Heineken, H., ‘Pairwise N-connected products of certain classes of finite groups’, Comm. Algebra
32 (2004), 4741–4752.CrossRefGoogle Scholar
Carocca, A., ‘A note on the product of F-subgroups in a finite group’, Proc. Edinb. Math. Soc.
39 (1996), 37–42.Google Scholar
Gállego, M. P., Hauck, P. and Pérez Ramos, M. D., ‘2-Engel relations between subgroups’, J. Algebra
447 (2016), 31–55.Google Scholar
Kim, Y. K. and Rhemtulla, A. H., ‘Weak maximality conditions and polycyclic groups’, Proc. Amer. Math. Soc.
123 (1995), 711–714.Google Scholar
Lennox, J. C. and Robinson, D. J. S., The Theory of Infinite Soluble Groups (Clarendon Press, Oxford, 2004).Google Scholar
Newman, M. F., ‘Some varieties of groups’, J. Aust. Math. Soc. Ser. A
16 (1973), 481–494.Google Scholar
Robinson, D. J .S., Finiteness Conditions and Generalized Soluble Groups (Springer, Berlin, 1972).Google Scholar
Robinson, D. J. S., ‘Splitting theorems for infinite groups’, Sympos. Math.
17 (1973), 441–470.Google Scholar
Traustason, G., ‘The local nilpotence theorem for 4-Engel groups revisited’, Int. J. Group Theory
4(3) (2015), 21–75.Google Scholar
Vaughan-Lee, M. R. and Wiegold, J., ‘Countable locally nilpotent groups of finite exponent without maximal subgroups’, Bull. Lond. Math. Soc.
13 (1981), 45–46.Google Scholar
Zel’manov, E., ‘On some problems of group theory and Lie algebras’, Math. USSR-Sb.
66 (1990), 159–168.Google Scholar
You have
Access